题目内容
18.甲质点以3m/s2的加速度从静止开始做匀加速直线运动,甲运动2S后,乙质点从同一起点以4m/s2的加速度从静止开始做同方向的匀加速直线运动,在乙追上甲之前,甲乙间的最大距离是( )| A. | 18m | B. | 23.5m | C. | 24m | D. | 28m |
分析 乙追上甲之前两车速度相等时两车相距最远,据速度时间关系求得相距最远距离.
解答 解:由相遇临界条件知,当乙车速度与甲车速度相等时两车相距最远,据速度时间关系知,此时乙车经过时间为t,则根据速度时间关系有:
v甲=v乙
即a甲(t+2)=a乙t代入数据有:3(t+2)=4t
解得:t=6s
此两两车相距$△x={x}_{甲}-{x}_{乙}=\frac{1}{2}×3×(6+2)^{2}-\frac{1}{2}×4×{6}^{2}$m=24m
故选:C.
点评 掌握追及相遇问题的临界条件速度相等时两车相距最远或最近,是正确解题的关键,不难.

练习册系列答案
相关题目
8.如图所示,一个小球被一根竖直细绳悬挂并紧靠在光滑斜面上,小球受力的个数为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.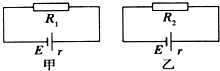 (多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
(多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
 (多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )
(多选)如图所示,甲、乙两电路中是两个完全相同的电源,定值电阻R1>R2.在两电路中分别通过相同电荷量q的过程中,下列判断正确的是( )| A. | 电源内部产生焦耳热较多的是乙电路 | |
| B. | R1上产生的焦耳热比R2上产生的焦耳热多 | |
| C. | 电源做功较多的是甲电路 | |
| D. | 甲、乙两电路中电源做功相等 |
13.在限速20km/h的地段,警察拦住一超速车对司机说:“先生,你刚才的车速是30km/h,已超速…”司机辩解说:“这段路很堵,我半小时才走5km,怎么会超速?…”以下观点不正确的是( )
| A. | 限速20km/h,表示该路段上行驶时,车辆允许的最大瞬时速度是20km/h | |
| B. | 从司机的辩解可以看出,司机可能没有弄清楚瞬时速度与平均速度的区别 | |
| C. | 物体在某位置的瞬时速度就是物体在该位置附近极短时间内的平均速度的极限 | |
| D. | 如果该司机真的由于堵车在半小时内才走5km,他不可能超速 |
10.关于磁感应强度的大小,下列说法正确的是( )
| A. | 一段通电导线在磁场中某处所受安培力越大,该处磁感应强度就越大 | |
| B. | 通电导线在磁场中受安培力为零处,磁感应强度一定为零 | |
| C. | 磁感线密集处磁感应强度就大 | |
| D. | 磁感应强度B反比于检验电流元IL |
7. 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )| A. | 甲、乙两物体都做匀速运动 | |
| B. | 乙做匀速运动,速度大小为12.5m/s | |
| C. | 甲、乙两物体运动8s后,在距甲的出发点60m处相遇 | |
| D. | 甲在运动过程中停了40s |
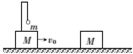 如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求
如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求