题目内容
【题目】如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内.若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度v0跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)运动员经过B点时速度的大小vB;
(2)运动员从台阶上A点跃出时的动能Ek;
(3)若初速度v0不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度v0的变化而变化.试在下面坐标系中粗略作出x﹣v0的图象,并标出图线与x轴的交点.
【答案】
(1)解:运动员从B点到D点做平抛运动
H﹣L= ![]() gt2①
gt2①
x=VBt ②
由①②式代入数据解得 VB=4.8m/s,
所以运动员经过B点时速度的大小为4.8m/s.
(2)解:运动员从A点到B点的过程中,由机械能守恒定律
mghAB= ![]() mVB2﹣Ek③
mVB2﹣Ek③
其中 hAB=L(1﹣cosθ) ④
由③④式代入数据解得 Ek=76J,
运动员从台阶上A点跃出时的动能Ek大小为76J.
(3)解:设运动员经O点正下方时的速度为VB′,B到水面的距离为h,则
![]() m
m ![]() ﹣
﹣ ![]() mV02=mg(H﹣Lcos37°﹣h) ⑤
mV02=mg(H﹣Lcos37°﹣h) ⑤
x=VB′ ![]() ⑥
⑥
由⑤⑥解得:x2﹣V02=20 ⑦
x﹣V0的图象如图所示:
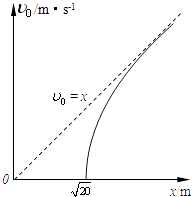
【解析】(1)运动员经过B点后做平抛运动,已知下落的高度h=H-L,由h=12gt2求出时间,由x=vBt求出运动员经过B点时速度vB的大小;
(2)从A运动到B的过程中,只有重力做功mgL(1-cosθ),根据动能定理求解运动员从A点跃出时的动能Ek.
【考点精析】解答此题的关键在于理解平抛运动的相关知识,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,以及对动能定理的综合应用的理解,了解应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷.

【题目】酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间.下表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车制动时的加速度大小都相同).
速度(m/s) | 思考距离/m | 制动距离/m | ||
正常 | 酒后 | 正常 | 酒后 | |
15 | 7.5 | 15.0 | 22.5 | 30.0 |
20 | 10.0 | 20.0 | 36.7 | 46.7 |
25 | 12.5 | 25.0 | 54.2 | x |
分析上表可知,下列说法正确的是( )
A.驾驶员酒后反应时间比正常情况下多1 s
B.若汽车以20 m/s的速度行驶时,发现前方40 m处有险情,酒后驾驶也能安全停车
C.汽车制动时,加速度大小约为7.5 m/s2
D.表中x为66.7