题目内容
13.某星球的半径为R,在该星球表面高H处自由释放一物体,经时间t落到该星球表面上,万有引力常量为G,不计一切阻力.求:(1)该星球表面的重力加速度;
(2)该星球的平均密度.
分析 (1)物体在星球表面做自由落体运动,其加速度即为星球表面的重力加速度,根据自由落体规律求得星球表面的重力加速度;
(2)由重力等于万有引力,求星球的质量,再求其密度.
解答 解:(1)物体在星球表面做自由落体运动,设星球表面的重力加速度为g,由自由落体运动规律,有:
H=$\frac{1}{2}g{t}^{2}$…①
解得:g=$\frac{2H}{{t}^{2}}$…②
(2)设该星球表面附近一物体质量为m,有:
G$\frac{Mm}{{R}^{2}}$=mg…③
星球的平均密度 ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$…④
联立解得:ρ=$\frac{3H}{2πGR{t}^{2}}$…⑤
答:(1)该星球表面的重力加速度是$\frac{2H}{{t}^{2}}$;
(2)该星球的平均密度是$\frac{3H}{2πGR{t}^{2}}$.
点评 掌握由自由落体求重加速度的方法,能根据重力等于万有引力,求天体的质量是常用的方法,是卡文迪许“称量地球质量”的原理.

练习册系列答案
相关题目
4.关子布朗运动.下列说法正确的是( )
| A. | 布朗远动就是液体分子的无规则运动 | |
| B. | 布朗运动是液体分子无规则运动的反映 | |
| C. | 布朗运动就是组成布朗微粒的固体分子的无规则运动 | |
| D. | 布朗运动是组成布朗微粒的固体分子无规则运动的反映 |
1.下列四个图象中,表示交变电流的是( )
| A. |  | B. |  | C. |  | D. |  |
3.随着我国登月计划的实施,我国航天员登上月球已不是梦想.假如我国航天员登上月球并在月球表面以初速度v0竖直向上抛出一个小球,经时间t后回到发出点.已知月球的半径为R,引力常量为G,则下列说法正确的是( )
| A. | 月球表面的重力加速度为$\frac{2{v}_{0}}{t}$ | |
| B. | 月球的质量为$\frac{2{v}_{0}{R}^{2}}{Gt}$ | |
| C. | 航天员在月球表面获得$\sqrt{\frac{{v}_{0}R}{t}}$的速度就可能离开月球表面围绕月球做圆周运动 | |
| D. | 航天员在月球表面附近绕月球做匀速圆周运动的绕行线速度为$\sqrt{\frac{{v}_{0}R}{t}}$ |
 如图所示,甲、乙两个交流电路中,两电源的输出电压和输出电流均相等,已知甲乙电路中两电阻的比值为4:1,则乙电路中理想变压器的原副线圈匝数比为4:1.
如图所示,甲、乙两个交流电路中,两电源的输出电压和输出电流均相等,已知甲乙电路中两电阻的比值为4:1,则乙电路中理想变压器的原副线圈匝数比为4:1.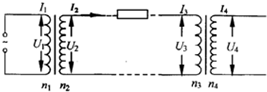
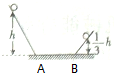 如图所示,小球从高为h的光滑斜面滚下,经粗糙的水平地面AB后再滚上另一光滑斜面,当它达到$\frac{1}{3}$h的高度时,速度减小为零,问小球最终停在何处?
如图所示,小球从高为h的光滑斜面滚下,经粗糙的水平地面AB后再滚上另一光滑斜面,当它达到$\frac{1}{3}$h的高度时,速度减小为零,问小球最终停在何处?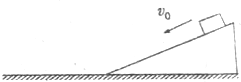 如图所示,用同种材料制成的倾角为37°的斜面和长水平面,斜面长11.25m且固定,一小物块从斜面顶端以初速度v0沿斜面下滑,如果v0=3.6m/s,则经过3.0s后小物块停在斜面上,不考虑小物块到达斜面底端时因碰撞损失的能量,求:(sin37°=0.6,cos37°=0.8)
如图所示,用同种材料制成的倾角为37°的斜面和长水平面,斜面长11.25m且固定,一小物块从斜面顶端以初速度v0沿斜面下滑,如果v0=3.6m/s,则经过3.0s后小物块停在斜面上,不考虑小物块到达斜面底端时因碰撞损失的能量,求:(sin37°=0.6,cos37°=0.8)