题目内容
质量m=1kg的小车左端放有质量M=3kg的铁块，两者以v0=4m/s的共同速度沿光滑水平面向竖直墙运动，车与墙的碰撞时间极短，无动能损失。铁块与车间的动摩擦因数为μ=1/3，车足够长，铁块不会到达车的右端。从小车第一次与墙相碰开始计时，取水平向右为正方向，g=10m/s2，求：（1）当小车和铁块再次具有共同速度时，小车右端离墙多远？（2）在答卷的图上画出第二次碰撞前，小车的速度时间图象。不要求写出计算过程，需在图上标明图线的起点、终点和各转折点的坐标。
（1）0.6m（2）（2）如图，要求：坐标系完整正确；
0~0.6s内图象及坐标完整正确；
0.6~0.9s内图象及坐标完整正确
0~0.6s内图象及坐标完整正确；
0.6~0.9s内图象及坐标完整正确
（1）撞墙后至两者具有共同速度，小车和铁块系统动量守恒：
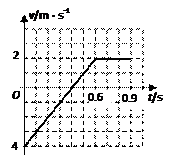
（M-m）v0=（M+m）v1，
此时小车右端离墙距离s1，由动能定理知：
，
。
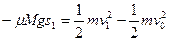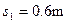（2）如图，要求：坐标系完整正确；
0~0.6s内图象及坐标完整正确；
0.6~0.9s内图象及坐标完整正确
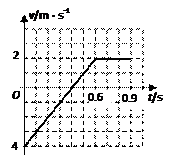
（M-m）v0=（M+m）v1，
此时小车右端离墙距离s1，由动能定理知：
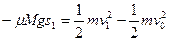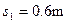，。 （2）如图，要求：坐标系完整正确；
0~0.6s内图象及坐标完整正确；
0.6~0.9s内图象及坐标完整正确
练习册系列答案
相关题目
)。A、B间夹着质量可忽略的火药。K为处于原长的轻质弹簧，两端分别连接住B和C。现点燃火药（此时间极短且不会影响各物体的质量和各表面的光滑程度），此后，发现A与D相碰后粘在一起，接着沿斜面前进了L =" 0.8" m 时速度减为零，此后设法让它们不再滑下。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5，取 g = 10 m/s2，sin37°= 0.6，cos37°= 0.8。求：
中，弹簧的最大弹性势能Ep。(弹簧始终未超出弹性限度)。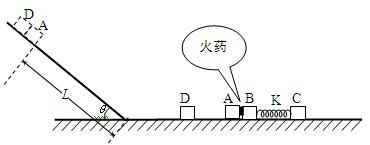
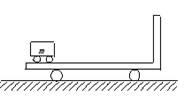
滑上B的左端，在右端与B碰撞后，最后恰好滑回木板B的左端. 已知
=3，并且在A与挡板碰撞时无机械能损失，忽略碰撞时间，取g=10m/s2，求：
