题目内容
5.如图a所示为“研究加速度与质量关系”的实验装置,小车和车上砝码的总质量为M,保持吊盘和盘中物块的总质量m不变,主要实验步骤如下: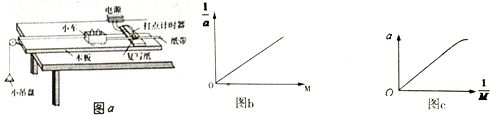
a.平衡摩擦力:先不放小吊盘,在长木板不带定滑轮的一端下面垫薄木块,并反复移动其位置,直到用手轻拨小车,打点计时器能在纸带上打出一系列均匀的点,关闭电源.
b.吊上小吊盘,放入适当的物块,将小车停在打点计时器附近,接通电源,后释放小车,打点计时器就在纸带上打下一系列的点,关闭电源.
c.改变小车中砝码的质量,重复步骤b.
d.在每条纸带上清晰的部分,每5个间隔标注一个计数点.测量相邻计数点的间距s1,s2,s3,???.求出相应的加速度a.
完成下列填空:
①如图给出的是实验中获取的一条纸带的一部分,A、B、C、D、E 是计数点,计数点间的距离如图所示,相邻计数点间时间间隔0.1s,根据图中数据可得,打下C点时小车的瞬时速度大小为0.48m/s,运动过程中小车的加速度大小为0.79m/s2(结果保留2位有效数字).

②设图b中的图线斜率为k,则吊盘和盘中物块的总质量m=$\frac{1}{kg}$.(用题中物理量的符号表示,重力加速度为g)
③甲同学以$\frac{1}{M}$为横坐标,a为纵坐标,在坐标纸上作出a-$\frac{1}{M}$的图线的示意图如图c所示,图线上部弯曲的原因是:没有满足M>>m.
分析 ①由平均速度表示中间时刻的瞬时速度,可得C点的瞬时速度.由逐差法可得加速度.
②当M>>m,吊盘和盘中物块的重力mg等于小车受到的拉力,由牛顿第二定律可得m;
③只有当M>>m,才能认为吊盘和盘中物块的重力mg等于小车受到的拉力.
解答 解:
①由平均速度表示中间时刻的瞬时速度,可得C点的瞬时速度为:${v}_{C}=\frac{{x}_{BD}}{2T}=\frac{0.044+0.052}{0.2}=0.48m/s$,
由逐差法可得:$a=\frac{{x}_{CE}-{x}_{AC}}{4{T}^{2}}=\frac{0.052+0.0598-0.0440-0.0362}{0.04}$=0.79m/s2,
②由牛顿第二定律可得:mg=Ma,解得:$m=\frac{Ma}{g}$,由图象斜率:$k=\frac{\frac{1}{a}}{M}=\frac{1}{aM}$,可得:$m=\frac{1}{kg}$.
③只有当M>>m,才能认为吊盘和盘中物块的重力mg等于小车受到的拉力,这样$a-\frac{1}{M}$的图线才会是直线,b图之所以出现弯曲是因为没有满足这一条件.
故答案为:①0.48;0.79;②$\frac{1}{kg}$;③没有满足M>>m.
点评 本题考查了打点计时器的应用以及根据纸带求物体运动的速度、加速度等问题,要熟练掌握从纸带上获取小车速度、加速度的方法,重点在于该实验的条件,要求M>>m,其次是对牛顿第二定律的灵活应用.

练习册系列答案
相关题目
4. 如图,质量为m的三角形尖劈静止于斜面上,上表面水平.今在其上表面加一竖直向下的力F,则物体( )
如图,质量为m的三角形尖劈静止于斜面上,上表面水平.今在其上表面加一竖直向下的力F,则物体( )
 如图,质量为m的三角形尖劈静止于斜面上,上表面水平.今在其上表面加一竖直向下的力F,则物体( )
如图,质量为m的三角形尖劈静止于斜面上,上表面水平.今在其上表面加一竖直向下的力F,则物体( )| A. | 保持静止 | B. | 向下匀速运动 | ||
| C. | 向下加速运动 | D. | 三种情况都有可能 |
16. 一带电粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的是( )
一带电粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的是( )
 一带电粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的是( )
一带电粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的是( )| A. | 粒子的速率一直增大 | B. | 粒子的加速度一直减小 | ||
| C. | 粒子的电势能一直增大 | D. | 以上说法均不正确 |
13.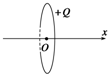 如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于x轴上的电场强度和电势的说法中正确的是( )
如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于x轴上的电场强度和电势的说法中正确的是( )
 如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于x轴上的电场强度和电势的说法中正确的是( )
如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于x轴上的电场强度和电势的说法中正确的是( )| A. | 从O点沿x轴正方向,电场强度增大,电势降低 | |
| B. | 从O点沿x轴正方向,电场强度减小,电势升高 | |
| C. | O点的电场强度为零,电势最低 | |
| D. | O点的电场强度为零,电势最高 |
20.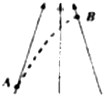 如图所示,实线表示某一电场的电场线.仅在电场力作用下,有一定初速度的一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
如图所示,实线表示某一电场的电场线.仅在电场力作用下,有一定初速度的一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
 如图所示,实线表示某一电场的电场线.仅在电场力作用下,有一定初速度的一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
如图所示,实线表示某一电场的电场线.仅在电场力作用下,有一定初速度的一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )| A. | 粒子带正电 | |
| B. | 粒子在A点加速度比B点小 | |
| C. | 粒子在A点速度比B点大 | |
| D. | 带电粒子在A点电势能比在B点的电势能大 |
14. 如图所示,真空中两虚线圆为以O为圆心的同心圆,分别于坐标轴交于abcd、efgh;在ac两点固定两个等量点电荷+Q,bd两点固定两个等量点电荷-Q.下列说法正确的是( )
如图所示,真空中两虚线圆为以O为圆心的同心圆,分别于坐标轴交于abcd、efgh;在ac两点固定两个等量点电荷+Q,bd两点固定两个等量点电荷-Q.下列说法正确的是( )
 如图所示,真空中两虚线圆为以O为圆心的同心圆,分别于坐标轴交于abcd、efgh;在ac两点固定两个等量点电荷+Q,bd两点固定两个等量点电荷-Q.下列说法正确的是( )
如图所示,真空中两虚线圆为以O为圆心的同心圆,分别于坐标轴交于abcd、efgh;在ac两点固定两个等量点电荷+Q,bd两点固定两个等量点电荷-Q.下列说法正确的是( )| A. | g、f两点的电场强度相同 | B. | e、h两点的电势相同 | ||
| C. | 将质子从e移到o电场力一直做正功 | D. | 将质子从o移到f电场力一直做正功 |
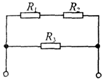 如图所示,电路中电阻R1:R2:R3=1:2:3,当电路中有电流通过时,电阻中电流之比I1:I2:I3=1:1:1,电阻两端电压之比U1:U2:U3=1:2:3.
如图所示,电路中电阻R1:R2:R3=1:2:3,当电路中有电流通过时,电阻中电流之比I1:I2:I3=1:1:1,电阻两端电压之比U1:U2:U3=1:2:3. 如图所示,光滑固定的竖直杆上套有一个质量m=0.4kg的小物块A,不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D,连接物块A和小物块B,虚线CD水平,间距d=0.72m,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.不计摩擦和空气阻力,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2.求:
如图所示,光滑固定的竖直杆上套有一个质量m=0.4kg的小物块A,不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D,连接物块A和小物块B,虚线CD水平,间距d=0.72m,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.不计摩擦和空气阻力,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2.求: