题目内容
9.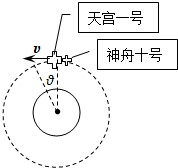 2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求:
2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求:(1)地球质量M;
(2)组合体运动的周期T;
(3)组合体所在圆轨道离地高度H.
分析 (1)在地球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$,由此即可求出地球的质量;
(2)t时间内组合体绕地球转过的角度为θ,结合$ω=\frac{θ}{t}$先求出角速度,然后再求出周期即可
(3)万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,可以解得组合体离地面的高度.
解答 解:(1)因为在地球表面的物体受到的重力等于万有引力,有:
$mg=G\frac{Mm}{{R}^{2}}$
解得:$M=\frac{g{R}^{2}}{G}$
(2)设组合体的角速度为ω,周期为T,则:$ω=\frac{θ}{t}$
T=$\frac{2π}{ω}=\frac{2πt}{θ}$
(3)万有引力提供向心力,得:$G\frac{Mm}{{(R+H)}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}(T+H)$
联立解得:H=$\root{3}{\frac{g{R}^{2}{t}^{2}}{{θ}^{2}}}-R$
答:(1)地球质量M是$\frac{g{R}^{2}}{G}$;
(2)组合体运动的周期T是$\frac{2πt}{θ}$;
(3)组合体所在圆轨道离地高度是$\root{3}{\frac{g{R}^{2}{t}^{2}}{{θ}^{2}}}-R$.
点评 本题关键是要掌握万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$和在地球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$这两个关系,并且要能够根据题意选择恰当的向心力的表达式.

练习册系列答案
相关题目
19. 如图所示,将两相同的木块a、b均静止在光滑水平面上,弹簧处于伸长状态,两细绳均有拉力,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b均静止在光滑水平面上,弹簧处于伸长状态,两细绳均有拉力,现将右侧细绳剪断,则剪断瞬间( )
 如图所示,将两相同的木块a、b均静止在光滑水平面上,弹簧处于伸长状态,两细绳均有拉力,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b均静止在光滑水平面上,弹簧处于伸长状态,两细绳均有拉力,现将右侧细绳剪断,则剪断瞬间( )| A. | a受到合外力为零 | B. | b受到合外力为零 | ||
| C. | 弹簧弹力为零 | D. | 左侧细绳拉力为零 |
20.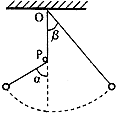 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,将悬线拉紧由钉子的右侧向左侧将小球拉起(悬绳会被钉子绑住).使悬绳与竖直方向成一角度a,然后由静止释放小球,小球向右摆动能达到的最大角度为B,则下结论正确的是( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,将悬线拉紧由钉子的右侧向左侧将小球拉起(悬绳会被钉子绑住).使悬绳与竖直方向成一角度a,然后由静止释放小球,小球向右摆动能达到的最大角度为B,则下结论正确的是( )
 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,将悬线拉紧由钉子的右侧向左侧将小球拉起(悬绳会被钉子绑住).使悬绳与竖直方向成一角度a,然后由静止释放小球,小球向右摆动能达到的最大角度为B,则下结论正确的是( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,将悬线拉紧由钉子的右侧向左侧将小球拉起(悬绳会被钉子绑住).使悬绳与竖直方向成一角度a,然后由静止释放小球,小球向右摆动能达到的最大角度为B,则下结论正确的是( )| A. | 小球的机械能守恒 | |
| B. | β=α | |
| C. | 小球经过最低点时水平向右的加速度将突然消失 | |
| D. | 小球经过最低点时悬线所受到的拉力将突然变大 |
17. 在如图所示的电路中,开关S原来时闭合的,现将S断开,则灯泡L亮度变化和电容器C带电量变化情况是( )
在如图所示的电路中,开关S原来时闭合的,现将S断开,则灯泡L亮度变化和电容器C带电量变化情况是( )
 在如图所示的电路中,开关S原来时闭合的,现将S断开,则灯泡L亮度变化和电容器C带电量变化情况是( )
在如图所示的电路中,开关S原来时闭合的,现将S断开,则灯泡L亮度变化和电容器C带电量变化情况是( )| A. | 灯泡L变亮、电容器C带电量增加 | B. | 灯泡L变亮、电容器C带电量减少 | ||
| C. | 灯泡L变暗、电容器C带电量增加 | D. | 灯泡L变暗、电容器C带电量减少 |
14.下列各组物理量均为矢量的是( )
| A. | 位移、时间、速度 | B. | 速度、加速度、路程 | ||
| C. | 力、速度、位移 | D. | 力、速度变化量、重力加速度、质量 |
18.原子质量单位为u,1u相当于931.5MeV的能量,真空中光速为c.当质量分别为m1 kg和m2 kg的原子核结合为质量为M kg的原子核时,释放出的能量是( )
| A. | (M-m1-m2)u•c2 J | B. | (m1+m2-M)c2 J | ||
| C. | (m1+m2-M)u×931.5 J | D. | (m1+m2-M)×931.5 eV |

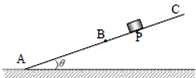 质量m=2kg的小物块置于倾角θ=37°的斜面上,A为斜面底端,斜面AB段的动摩擦因数μ=0.8,BC段光滑,AB段长度为5m,PB段长为3m,现把物块从P点由静止释放,已知:sin37°=0.6,cos37°=0.8.g取10m/s2.求
质量m=2kg的小物块置于倾角θ=37°的斜面上,A为斜面底端,斜面AB段的动摩擦因数μ=0.8,BC段光滑,AB段长度为5m,PB段长为3m,现把物块从P点由静止释放,已知:sin37°=0.6,cos37°=0.8.g取10m/s2.求