题目内容
有一个推饮料瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段距离后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败。其简化模型如图所示,AD为水平桌面,选手们可将瓶子放在A点,从A点开始用一水平恒力推瓶,推到B点放手,让瓶子沿AD做直线运动,CD为有效区域。已知A、B、C、D间长度分别为L1=0.3m,L2 =3.2m,L3 =0.5m,瓶子质量为m=l kg,瓶子与桌面间的动摩擦因数为μ=0.3。假设瓶子可视为质点,滑行过程中未倒下,g取10m/s2,试问:
(1)某选手把瓶推到B点放手时,瓶的速度vB=4m/s,则该选手在游戏中能否成功,请计算说明?
(2)选手要想在游戏中获得成功,水平推力F的最大值不得超过多少?
(1)某选手把瓶推到B点放手时,瓶的速度vB=4m/s,则该选手在游戏中能否成功,请计算说明?
(2)选手要想在游戏中获得成功,水平推力F的最大值不得超过多少?

解:(1)设瓶运动的最远距离为s,由功能关系得:
μmgs=
得s=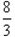 m<3.2m,所以不能成功
m<3.2m,所以不能成功
(2)游戏要想获得成功,瓶滑到D点速度恰好为0,从A到D,由动能定理得
FmaxL1-μmg(L1+L2+ L3)=0
解得Fmax=40N
μmgs=

得s=
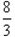 m<3.2m,所以不能成功
m<3.2m,所以不能成功(2)游戏要想获得成功,瓶滑到D点速度恰好为0,从A到D,由动能定理得
FmaxL1-μmg(L1+L2+ L3)=0
解得Fmax=40N

练习册系列答案
相关题目