题目内容
【题目】某同学为了探究物体在斜面上运动时摩擦力与斜面倾角的关系,设计实验装置如图乙所示,长直平板一端放在水平桌面上,另一端架在一物块上,在平板上标出A、B两点,B点处置一光电门,用光电计时器记录滑块通过光电门时挡光的时间,实验步骤如下:
①用游标卡尺测量滑块的挡光长度d,用天平测量滑块的质量m;
②用直尺测量AB之间的距离s,A点到水平桌面的垂直距离h1 , B点到水平桌面的垂直距离h2;
③将滑块从A点由静止释放,从光电计时器读出滑块的挡光时间t1;
④重复步骤③数次,并求挡光时间的平均值 ![]() ;
;
⑤利用所测数据求出摩擦力f和斜面倾角的余弦值cosα;
⑥多次改变斜面的倾角,重复实验步骤②③④⑤,做出f﹣cosα关系曲线.
(1)测量滑块挡光长度的游标卡尺读数如图甲所示,读得d=cm
(2)(用测量的物理量表示下列各式,重力加速度为g)
①滑块运动时所受到的摩擦阻力f= .
②若f﹣cosα关系曲线的斜率为k,则动摩擦因数可表示为μ= . 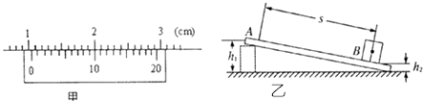
【答案】
(1)1.050
(2)mg ![]() ﹣m
﹣m ![]() ;
;![]()
【解析】解:(1)游标卡尺的主尺读数为10mm,游标尺上第10个刻度与主尺上某一刻度对齐,故其读数为10×0.5mm=5.0mm,
所以最终读数为:10mm+5.0mm=10.50mm=1.050cm;(2)①滑块通过光电门时的速度:v= ![]() ;
;
由v2﹣v02=2ax可得:v2=2as,
即:( ![]() )2=2as,
)2=2as,
解得加速度为:a= ![]() ;
;
由牛顿第二定律得:mgsinθ﹣f=ma,
其中sinθ= ![]() ,
,
解得:f=mg ![]() ﹣m
﹣m ![]() ;
;
②滑动摩擦力f=μmgcosα,故在f﹣cosα图像中,斜率k=μmg,故 ![]()
所以答案是:(1)1.050;(2)mg ![]() ﹣m
﹣m ![]() ;②
;② ![]()
【考点精析】利用滑动摩擦力对题目进行判断即可得到答案,需要熟知滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解.