题目内容
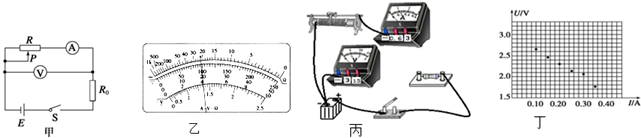
7.验证机械能守恒定律实验装置如图甲所示,某小组完成一系列实验操作后,得到了一条纸带如图乙所示,图中O是打点计时器打的第一个点,用刻度尺测量连续的计时点A、B、C、D、E、F到O点的距离分别是h1、h2、h3、h4、h5、h6(1)已知打点计时器的打点周期为T,可求出B、C、D、E各计数点对应小车的速度,其中E点时小车运动的速度为vE=$\frac{{h}_{6}-{h}_{4}}{2T}$,小车运动的加速度a=$\frac{{(h}_{3}-{h}_{2})-({h}_{2}-{h}_{1})}{{T}^{2}}$(用h1、h2、h3和T表示).

(2)测出重物下落的高度h和小车运动的速度v,并用天平测出重物和小车质量分别为M和m,已知当地的重力加速度为g,则验证系统机械能守恒的表达式为Mgh=$\frac{1}{2}$(m+M)v2,利用测出的数据作出$\frac{v^2}{2}-h$图象如图丙所示,则当图线的斜率接近$\frac{M}{M+m}g$时,即可验证系统机械能守恒.
(3)本实验中产生的误差的可能原因是小车及纸带受到的摩擦阻力或系统受到的空气阻力.
分析 (1)根据E点的速度等于DF段的平均速度列式可求得E点的速度;根据△X=aT2可求得加速度;
(2)分析系统中能量的转化规律,根据机械能守恒定律可得出对应的表达式,再分析图象即可明确如何验证机械能守恒;
(3)根据实验原理明确实验误差的来源.
解答 解:(1)E点的速度等于DF段的平均速度,故vE=$\frac{{h}_{6}-{h}_{4}}{2T}$;
根据△X=aT2可得:
a=$\frac{{(h}_{3}-{h}_{2})-({h}_{2}-{h}_{1})}{{T}^{2}}$
(2)重物下落过程拉动小车运动,由于重物的重力势能减小,而重物和小车的动能增加,则由机械能守恒定律可知:
Mgh=$\frac{1}{2}$(M+m)v2;
则可知$\frac{{v}^{2}}{2}$=$\frac{Mg}{M+m}h$
则由图形可知:只要k=$\frac{M}{M+m}g$即可验证机械能守恒定律;
(3)由于本实验中小车和纸带受到摩擦力,并且重物及小车均受到空气阻力,因此存在误差;
故答案为:(1)$\frac{{h}_{6}-{h}_{4}}{2T}$; $\frac{{(h}_{3}-{h}_{2})-({h}_{2}-{h}_{1})}{{T}^{2}}$; (2)Mgh=$\frac{1}{2}$(M+m)v2;
$\frac{M}{M+m}g$; (3)小车及纸带受到的摩擦阻力或系统受到的空气阻力
点评 本题考查验证机械能守恒定律的探究性实验,要注意认真分析实验装置,明确实验原理,再根据我们所熟知的纸带处理方法进行分析处理即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.对下列所述涉及的物理思想与方法的说法,不正确的是( )
| A. | 根据v=$\frac{△s}{△t}$,当△t非常小时,$\frac{△s}{△t}$就可以表示物体在t时刻的瞬时速度,当中用到了极限的思想 | |
| B. | 在不需要考虑物体本身大小和形状时,可以用质点来代替物体,这是假设法 | |
| C. | 借助激光器及平面镜观察桌面的微小形变的实验中,运用了放大的思想 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
18.从足够高处释放一石子甲,经0.8s,从同一位置再释放另一石子乙,不计空气阻力,则在两石子落地前,下列说法中正确的是( )
| A. | 它们间的距离与乙石子运动的时间成正比 | |
| B. | 它们间的距离保持不变 | |
| C. | 它们在空中运动的时间相同 | |
| D. | 它们在空中运动的时间与其质量有关 |
15.下列关于重力、弹力、摩擦力的说法中正确的时( )
| A. | 地面附近物体所受到的重力就是地球对物体的吸引力 | |
| B. | 用弹簧测力计可以直接测出物体的重力 | |
| C. | 滑动摩擦力的方向可以与物体运动的方向相同 | |
| D. | 物体间的弹力越大,则摩擦力越大 |
16.质子和α粒子在同一匀强磁场中做半径相同的匀速圆周运动.由此可知质子的动量P1和α粒子的动量P2之比P1:P2为( )
| A. | 1:1 | B. | 4:1 | C. | 1:2 | D. | 2:1 |
16.一个阻值为10Ω的电阻,通过它的电流强度为0.5A,则下列说法正确的是( )
| A. | 该电阻两端的电压是10V | B. | 该电阻20s内的发热量为50J | ||
| C. | 该电阻1s内的发热量为5J | D. | 该电阻发热功率为50W |
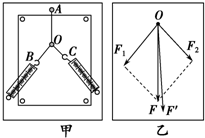 在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某一点并记下该点的位置;再将橡皮条的另一端系两根细绳(绳另一端都有绳套),用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条.
在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某一点并记下该点的位置;再将橡皮条的另一端系两根细绳(绳另一端都有绳套),用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条.