题目内容
14.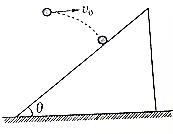 如图所示,宇航员站在某治质量分布均匀的星球表面以初速度v0水平抛出一个小球,小球飞行一段时间t后恰好垂直地撞在倾角为θ的该星球表面的斜坡上.已知该星球的半径为R,不考虑其它可能存在的阻力.求:
如图所示,宇航员站在某治质量分布均匀的星球表面以初速度v0水平抛出一个小球,小球飞行一段时间t后恰好垂直地撞在倾角为θ的该星球表面的斜坡上.已知该星球的半径为R,不考虑其它可能存在的阻力.求:(1)该星球表面的重力加速度;
(2)该星球的第一宇宙速度.
分析 (1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平抛运动的规律求出星球表面的重力加速度.
(2)第一宇宙速度的大小等于贴近星球表面运行的速度.根据万有引力提供向心力求出第一宇宙速度的大小
解答 解:(1)物体落在斜面上:$tanθ=\frac{{v}_{0}}{gt}$ 则$;g=\frac{{v}_{0}}{tanθ•t}$
(2)根据万有引力提供向心力得:mg=m$\frac{{v}^{2}}{R}$ 则v=$\sqrt{gR}=\sqrt{\frac{{v}_{0}R}{tanθ•t}}$
答:(1)该星球表面的重力加速度为$\frac{{v}_{0}}{tanθ•t}$
(2)该星球的第一宇宙速度为$\sqrt{\frac{{v}_{0}R}{tanθ•t}}$
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能灵活运用

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
9.如图所示的金属圆环放在有界匀强磁场中,将它从磁场中匀速拉出的过程中,下列说法正确的是( )
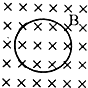

| A. | 向左拉出和向右拉出,其感应电流方向相反 | |
| B. | 不管从什么方向拉出,环中的感应电流总是逆时针方向 | |
| C. | 不管从什么方向拉出,环中的感应电流总是顺时针方向 | |
| D. | 在匀速拉出过程中感应电流大小不变 |
19.关于第一宇宙速度的说法中正确的是( )
| A. | 第一宇宙速度是发射卫星的最大速度 | |
| B. | 第一宇宙速度的数值是11.2km/s | |
| C. | 第一宇宙速度是近地绕地卫星应具有的速度 | |
| D. | 第一宇宙速度是卫星做圆周运动的最小线速度 |
3.A、B、C三点在同一直线上,AB:BC=1:2,B点位于A、C之间,在B处固定一电荷量为Q的点电荷.当在A处放一电荷量为+q的点电荷时,它所受到的电场力为F;移去A处电荷,在C处放一电荷量为-2q的点电荷,其所受电场力为( )
| A. | $-\frac{F}{2}$ | B. | -F | C. | $\frac{F}{2}$ | D. | F |
4.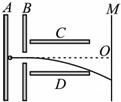 如图所示,平行金属板A、B间加速电压为U1,C、D间的偏转电压为U2,M为荧光屏.今有不计重力的一价氢离子(H+)和二价氦离子(He2+)的混合体,从A板由静止开始经加速和偏转后,打在荧光屏上,则它们( )
如图所示,平行金属板A、B间加速电压为U1,C、D间的偏转电压为U2,M为荧光屏.今有不计重力的一价氢离子(H+)和二价氦离子(He2+)的混合体,从A板由静止开始经加速和偏转后,打在荧光屏上,则它们( )
 如图所示,平行金属板A、B间加速电压为U1,C、D间的偏转电压为U2,M为荧光屏.今有不计重力的一价氢离子(H+)和二价氦离子(He2+)的混合体,从A板由静止开始经加速和偏转后,打在荧光屏上,则它们( )
如图所示,平行金属板A、B间加速电压为U1,C、D间的偏转电压为U2,M为荧光屏.今有不计重力的一价氢离子(H+)和二价氦离子(He2+)的混合体,从A板由静止开始经加速和偏转后,打在荧光屏上,则它们( )| A. | 同时到达屏上同一点 | B. | 先后到达屏上同一点 | ||
| C. | 同时到达屏上不同点 | D. | 先后到达屏上不同点 |
 在“探究加速度与力、质量的关系”实验中,采用如图1所示的实验装置,小车及车载砝码的质量用M表示,盘及盘中砝码的质量用m表示.
在“探究加速度与力、质量的关系”实验中,采用如图1所示的实验装置,小车及车载砝码的质量用M表示,盘及盘中砝码的质量用m表示.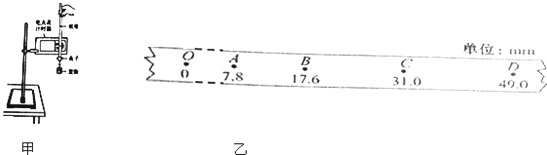
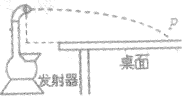 2015年第53届世界乒乓球锦标赛在我国苏州举行,中国健儿在比赛中取得了十分优异的成绩,这些成绩的背后是运动员刻苦的训练和顽强的拼搏,如图所示是运动员训练时用的乒乓球发射器示意图,发射口距桌面高度为h=0.45m,假定乒乓球水平射出,落在桌面上与发射口水平距离x=2.4m的P点,飞行过程中未触网,乒乓球质量m=0.0027kg,不计空气阻力,取g=10m/s2,求:
2015年第53届世界乒乓球锦标赛在我国苏州举行,中国健儿在比赛中取得了十分优异的成绩,这些成绩的背后是运动员刻苦的训练和顽强的拼搏,如图所示是运动员训练时用的乒乓球发射器示意图,发射口距桌面高度为h=0.45m,假定乒乓球水平射出,落在桌面上与发射口水平距离x=2.4m的P点,飞行过程中未触网,乒乓球质量m=0.0027kg,不计空气阻力,取g=10m/s2,求: 如图所示的是为纪念发现“磁生电”现象的物理学家法拉第而发行的一枚邮票,该发现导致了世界上第一台发电机的产生,从而把人类社会带进了电气化时代.
如图所示的是为纪念发现“磁生电”现象的物理学家法拉第而发行的一枚邮票,该发现导致了世界上第一台发电机的产生,从而把人类社会带进了电气化时代.