题目内容
一位同学家住25层的高楼上,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度。他将台秤放在电梯内,将重物放在台秤托盘上,电梯从第一层开始启动,经过不间断的运行,最后停在最高层。在整个过程中,他记录了台秤在不同时间段示数,记录的示数如下表所示;0—3.0 s时间段内台秤的示数也是稳定的。(g取10 m/s2)(1)电梯在0—3.0 s时间段内台秤的示数应该是多少?
(2)根据测量的数据,计算该座楼房每一层的平均高度。
时间(s) | 台秤示数(kg) |
电梯启动前 | 5.0 |
3.0—13.0 | 5.0 |
13.0—19.0 | 4.6 |
19.0以后 | 5.0 |
解:(1)电梯启动前,台秤示数为5.0 kg,则物体重力G=mg=50 N。由于表中各段时间内台秤示数恒定,所以在时间t1(0—3.0 s)内,物体做匀加速运动,在时间t2(3.0—13.0 s)内物体做匀速直线运动,在时间t2(13.0—19.0s)内物体做匀减速直线运动,19.0 s未度减为零。在13.0—19.0 s内,物体所受的支持力N3=46 N。根据牛顿第二定律,有mg—N3=ma3;13.0 s末物体的速度v=a3t3 ;由于电梯在13.0 s末的速度与3.0 s末的速度相同,因此,物体在0—3 s内的加速度a1=v2/t=v3/t1 ;由牛顿第二定律有N1-mg=ma1 ;由以上各式代入已知数据解得:N1=58N ;所以台秤的示数为5.8 kg
(2)电梯在0—3 s内的位移为s1=a1t12/2 ;3.0—13.0 s内物体的位移为s2=v2t2 ;13.0—19.0 s内物体的位移为s3=v2t3/2 ;所以楼房的总高度H=s1+s2+s3;由以上各式代入已知数据可得:H=69.6 m;所以平均每层的楼高人:H/24=2.9m

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
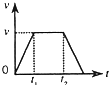 一位同学家住25层的高楼上,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内,将重物放在台秤托盘上,电梯从第一层开始启动,经过不间断的运行.最后停在最高层.在整个过程中.他记录了
一位同学家住25层的高楼上,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度.他将台秤放在电梯内,将重物放在台秤托盘上,电梯从第一层开始启动,经过不间断的运行.最后停在最高层.在整个过程中.他记录了