题目内容
（2013四川攀枝花第二次统考）如图所示，静放在水平面上的
圆形（半径为R）光滑管道ABC，C为最高点，B为最低点,管道在竖直面内。管道内放一小球，小球可在管道内自由移动，现用一装置将小球锁定在P点，过P点的半径OP与竖直方向的夹角为θ。现对管道施加一水平向右的恒力F，同时解除对小球的锁定，管道沿水平面向右做匀加速运动，小球相对管道仍保持静止。经过一段时间后管道遇一障碍物突然停止运动，小球能到达管道的A点。重力加速度为g，小球及管道大小不计。求：
（1）恒力作用下圆形管道运动的加速度；
（2）圆形管道从开始运动到突然停止过程中运动距离的可能值。
解：(1)小球受力如图，由力合成的平行四边形定则及牛顿第二定律得：
（2分）
（1分）
（2）设圆形管道从开始运动
到突然停止，停止前速度为
，由匀变速运动公式得：
（2分）
圆形管道停止时，小球沿管道半径方向的速度变为零，沿切线方向的速度保持不变，小球能运动到管道右侧圆心上方至最高点C之间的区域则可到达A点，或从C点飞出做平抛运动到达A点。
若小球能运动到管道右侧圆心上方至最高点C之间的区域，则由机械能守恒得：
（5分）
联立以上相关各式得：
（2分）
若小球从C点飞出做平抛运动到达A点，则由机械能守恒及平抛运动规律得：
（2分）
（3分）
联立以上相关各式得：
（2分）
圆形管道从开始运动到突然停止过程中运动距离的可能值为：
及 （1分）
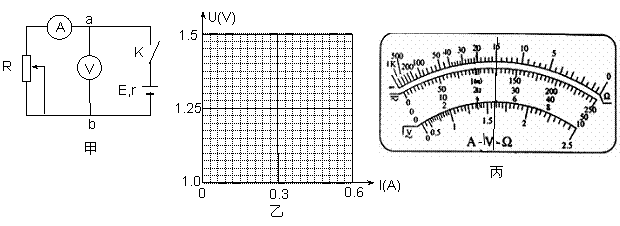
阅读快车系列答案（2013四川攀枝花二模）如图甲为《测量电源电动势和内电阻》的实验电路图，某同学按实验电路测量记录如下
| 1 | 2 | 3 | 4 | 5 | |
| Ｕ（V） | 1.40 | 1.35 | 1.25 | 1.10 | 1.00 |
| I （A） | 0.12 | 0.24 | 0.27 | 0.45 | 0.57 |
① 请在答题卡图中画出U–I图,并根据图线求出电动势E＝__ _V(保留两位有效数字)，内电阻r＝_ __Ω(保留一位有效数字)。
② 若实验室没有合适的电压表，某同学用老师提供的多用电表测量电压，实验时多用电表黑表笔应连接图甲中的 (填a或b)，某次测量时多用表档位开关置于直流电压2.5Ｖ档，示数如图丙所示，此时电源路端电压为 Ｖ。
的半圆形玻璃砖置于光屏MN的上方，其平面AB与MN的距离h=10cm。一束单色光沿图示方向射向圆心O，经玻璃砖后射到光屏上的O′点。现使玻璃砖绕圆心O点逆时针转动，下列关于光屏上光点的移动方向，距O′点的最远距离的说法，正确的是 
、
、
，它们的轨道半径分别为
、
、
，且