��Ŀ����
����Ŀ����һ���ƿ�Ȫˮƿ����Ϸ��Ŀ�������ǣ�ѡ���Ǵ���㿪ʼ������ƿһ��ʱ�������ƿ��ǰ��������ƿ���ͣ��������Ч�����ڣ���Ϊ�ɹ�����ƿ���δͣ��������Ч�����ڻ��ڻ��й����е��£�����Ϊʧ�ܣ����ģ����ͼ��ʾ��AC�dz���ΪL1=5m��ˮƽ���棬ѡ���ǿɽ�ƿ�ӷ���A�㣬��A�㿪ʼ��һ�㶨�����ˮƽ������ƿ��BCΪ��Ч������֪BC����L2=1m��ƿ������m=0.5kg��ƿ���������Ķ�Ħ��������=0.4��ijѡ��������ƿ���ϵ�ˮƽ����F=20N��ƿ����AC��ֱ���˶�������ƿ�ӿ���Ϊ�ʵ㣬gȡ10m/s2 �� ��ô��ѡ��Ҫ����Ϸ��óɹ������ʣ�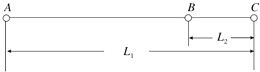
��1������������ƿ���ϵ�ʱ������ó������٣�
��2������������ƿ���ϵľ�����СΪ���٣�
���𰸡�
��1���⣺Ҫ������Ϸ�ɹ���ƿ����C���ٶ�����Ϊ0��������ʱ������������ʱ��Ϊt1��
��������ʱƿ�ļ��ٶ�Ϊa1��t1ʱ��ƿ���ٶ�Ϊv����ֹͣ����ٶ�Ϊa2����ţ�ٵڶ����ɵã�
F����mg=ma1 �٦�mg=ma2 ��
�����˶������е�λ�ƣ�x1= ![]() ��
��
�����˶������е�λ�ƣ�x2= ![]() ��
��
λ�ƹ�ϵ���㣺x1+x2=L1 ���֣�v=a1t1 ��
�����ϸ�ʽ��ã�t1= ![]() s
s
������������ƿ���ϵ�ʱ������ó��� ![]() s
s
��2���⣺Ҫ����Ϸ��óɹ���ƿ����B ���ٶ�����Ϊ�㣬�����þ�����С������С����Ϊd��
�� ![]() +
+ ![]() =L1��L2��
=L1��L2��
v��2=2a1d ��
������ã�d=0.4m
������������ƿ���ϵľ�����СΪ0.4m
����������1�������������ȸ���ţ�ٵڶ���������ƿ�Ӽ��ٺͼ���ʱ�ļ��ٶȣ�Ȼ������˶�ѧ��ʽ��ϼ��ι�ϵ��ʽ����ƿ��ǡ�û�����C��ʱ����������ʱ�䣻��2��ƿ��ǡ�û�����B�㣬���������þ�����̣������˶�ѧ��ʽ��ϼ��ι�ϵ��ʽ��⼴�ɣ�