题目内容
 (2009?扬州模拟)如图所示,质量为m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为l,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ角的A点.已知静电力恒量为k.求:
(2009?扬州模拟)如图所示,质量为m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为l,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ角的A点.已知静电力恒量为k.求:(1)小球静止在A点处绳子受到的拉力的大小;
(2)外加电场场强的大小;
(3)将小球拉起至与O点等高的B点后无初速释放,则小球经过最低点C时绳受到的拉力.
分析:对小球进行受力分析,根据共点力平衡,抓住合力等于零,运用正交分解求出拉力大小和电场力大小,从而求出电场强度.
根据动能定理求出运动到最低点的速度,沿半径方向上的合力提供向心力,根据牛顿第二定律求出绳受到的拉力T2大小.
根据动能定理求出运动到最低点的速度,沿半径方向上的合力提供向心力,根据牛顿第二定律求出绳受到的拉力T2大小.
解答: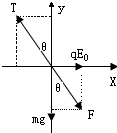 解:(1)带电小球A处于平衡,其受力如图,其中F为两点电荷间的库仑力,
解:(1)带电小球A处于平衡,其受力如图,其中F为两点电荷间的库仑力,
T为绳子拉力,F0为外加电场给A的电场力,则
Tcosθ-mg-Fcosθs=0 ①
Fsinθ+F0-Tsinθ=0 ②
F=k
联立式解得 T1=k
+
(2)E=
=
(3)小球从B运动到C的过程中,Q对q的库仑力不做功,由动能定理得
mgl-qEl=
mυC2-0
在C点时 T2-k
-mg=m
联立解得 T2=k
+mg(3-2tanθ)
答:(1)小球在A点绳子受到的拉力为k
+
(2)电场强度为
.
(3)绳受到的拉力T2大小为k
+mg(3-2tanθ)
 解:(1)带电小球A处于平衡,其受力如图,其中F为两点电荷间的库仑力,
解:(1)带电小球A处于平衡,其受力如图,其中F为两点电荷间的库仑力,T为绳子拉力,F0为外加电场给A的电场力,则
Tcosθ-mg-Fcosθs=0 ①
Fsinθ+F0-Tsinθ=0 ②
F=k
| l2 |
联立式解得 T1=k
| l2 |
| mg |
| cosθ |
(2)E=
| F |
| q |
| mgtanθ |
| q |
(3)小球从B运动到C的过程中,Q对q的库仑力不做功,由动能定理得
mgl-qEl=
| 1 |
| 2 |
在C点时 T2-k
| l2 |
| ||
| l |
联立解得 T2=k
| l2 |
答:(1)小球在A点绳子受到的拉力为k
| l2 |
| mg |
| cosθ |
(2)电场强度为
| mgtanθ |
| q |
(3)绳受到的拉力T2大小为k
| l2 |
点评:本题考查了共点力平衡问题、动能定理以及牛顿第二定律,知道小球做圆周运动沿半径方向上的合力提供向心力.

练习册系列答案
相关题目
 (2009?扬州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf平面与电场平行,bedf平面与电场垂直,则下列说法中正确的是( )
(2009?扬州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf平面与电场平行,bedf平面与电场垂直,则下列说法中正确的是( ) (2009?扬州模拟)如图所示,在一个质量不计的定滑轮上穿过一根质量为m的环形链条,在链条竖直部分有一只质量为M的猴子拉着链条开始向上爬,并保持高度不变,则猴子的输出功率随时间变化的关系是下图中的( )
(2009?扬州模拟)如图所示,在一个质量不计的定滑轮上穿过一根质量为m的环形链条,在链条竖直部分有一只质量为M的猴子拉着链条开始向上爬,并保持高度不变,则猴子的输出功率随时间变化的关系是下图中的( ) (2009?扬州模拟)如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L则( )
(2009?扬州模拟)如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L则( ) (2009?扬州模拟)一环状物体套在光滑水平直杆上,能沿杆自由滑动,绳子一端系在物体上,另一端绕过定滑轮,用大小恒定的力F拉着,使物体沿杆自左向右滑动,如图所示,物体在杆上通过a、b、c三点时的动能分别为Ea、Eb、Ec,且ab=bc,滑轮质量和摩擦均不计,则下列关系中正确的是( )
(2009?扬州模拟)一环状物体套在光滑水平直杆上,能沿杆自由滑动,绳子一端系在物体上,另一端绕过定滑轮,用大小恒定的力F拉着,使物体沿杆自左向右滑动,如图所示,物体在杆上通过a、b、c三点时的动能分别为Ea、Eb、Ec,且ab=bc,滑轮质量和摩擦均不计,则下列关系中正确的是( )