题目内容
8. 一透明球体置于空气中,球半径R=10cm,MN是一条通过球心O的直线,单色细光束AB平行于MN射向球体,B点为入射点,入射角为45°,CD为出射光线,C点为出射点,CD与MN所夹的角α=30°,求:
一透明球体置于空气中,球半径R=10cm,MN是一条通过球心O的直线,单色细光束AB平行于MN射向球体,B点为入射点,入射角为45°,CD为出射光线,C点为出射点,CD与MN所夹的角α=30°,求:①透明球体的折射率n;
②光从B点传到C点所需的时间t.
分析 连接OB、BC,在B点光线的入射角、折射角分别标为i、r,作出光路图,根据几何关系求出入射角与折射角,根据折射定律求解折射率,
再依据公式v=$\frac{c}{n}$,结合几何关系,求解所需要的时间.
解答 解:①连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示. 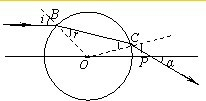
在△OCP中:有$\frac{OC}{sinα}$=$\frac{OP}{sin∠OCP}$
由题意有:OP=$\sqrt{2}$OC,α=30°
解得:∠OCP=135°(45°值舍去)
进而可得:∠COP=180°-α-∠OCP=180°-135°-30°=15°
光线从B点射入,由折射定律有:n=$\frac{sini}{sinr}$
光线从C点射出,由折射定律有:n=$\frac{sin(180°-135°)}{sin∠BCO}$,
又∠BCO=r
i=45°
又∠BOC=180°-i-∠COP=120°=180°-45°-15°=120°,
故得:r=$\frac{1}{2}$(180°-∠BOC)=$\frac{1}{2}$×(180°-120°)=30°
因此,透明体的折射率n=$\frac{sini}{sinr}$=$\frac{sin45°}{sin30°}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$
②根据几何关系,则有:SBC=2Rcos30°
那么光在玻璃中的传播速度v=$\frac{c}{n}$;
因此光从B点传到C点所需的时间t=$\frac{{S}_{BC}}{v}$=$\frac{n{S}_{BC}}{c}$
代入数据,解得:t=$\frac{\sqrt{6}}{3}×1{0}^{-9}s$
答:①透明球体的折射率$\sqrt{2}$;
②光从B点传到C点所需的时间$\frac{\sqrt{6}}{3}×1{0}^{-9}s$.
点评 本题是较为复杂的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解,折射过程中频率不变.

 同步奥数系列答案
同步奥数系列答案 如图所示,在半圆形光滑凹槽内,两轻质弹簧的下端固定在槽的最低点,另一端分别与小球P、Q相连.已知两球在图示P、Q位置静止.则下列说法中正确的是( )
如图所示,在半圆形光滑凹槽内,两轻质弹簧的下端固定在槽的最低点,另一端分别与小球P、Q相连.已知两球在图示P、Q位置静止.则下列说法中正确的是( )| A. | 若两球质量相同,则P球对槽的压力较小 | |
| B. | 若两球质量相同,则两球对槽的压力大小相等 | |
| C. | 若P球的质量大,则O′P弹簧的劲度系数大 | |
| D. | 若P球的质量大,则O′P弹簧的弹力大 |
 如图,用两条同样的绳子拉一物体,物体受到的重力为G,两绳受到的拉力分别为F1、F2夹角为θ
如图,用两条同样的绳子拉一物体,物体受到的重力为G,两绳受到的拉力分别为F1、F2夹角为θ
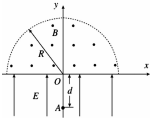 如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场.磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B,y轴下方的A点与O点的距离为d,一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.粒子重力不计.求:
如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场.磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B,y轴下方的A点与O点的距离为d,一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.粒子重力不计.求:
 如图所示,倾角为37°的斜面上,轻弹簧一端固定在A点,弹簧处于自然状态时另一端位于B点,斜面上方有半径为R=1m、圆心角为143°的竖直圆弧形光滑轨道与斜面相切于D处,圆弧轨道的最高点为M.现用一质量为m=1kg的小物块(可视为质点)沿斜面将轻弹簧压缩40cm到C点由静止释放,物块经过B点后在BD段运动时的位移与时间关系为x=8t-4.5t2(x的单位是m,t的单位是s).若物块经过D点后恰好能到达M点,取g=10m/s2,sin37°=0.6,求:
如图所示,倾角为37°的斜面上,轻弹簧一端固定在A点,弹簧处于自然状态时另一端位于B点,斜面上方有半径为R=1m、圆心角为143°的竖直圆弧形光滑轨道与斜面相切于D处,圆弧轨道的最高点为M.现用一质量为m=1kg的小物块(可视为质点)沿斜面将轻弹簧压缩40cm到C点由静止释放,物块经过B点后在BD段运动时的位移与时间关系为x=8t-4.5t2(x的单位是m,t的单位是s).若物块经过D点后恰好能到达M点,取g=10m/s2,sin37°=0.6,求: