题目内容
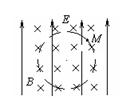
如图所示,虚线 1l、l2将无重力场的空间分成三个区域, I 区内存在水平向右的匀强电场 E1和垂直纸面向里的匀强磁场 Bl , Ⅱ区内以水平线 CO 为分界,上方存在着竖直向上的匀强电场E2,下方存在着竖直向下的匀强电场E3 Ⅲ 区内存在以l2为左边界、右边无界的垂直纸面向里的匀强磁场B2,在 I 区内有一段粗糙、长为 L 的水平放置塑料直管道 AC ,一可视为质点的带正电小球(直径比管内径略小)的质量为 m 、带电量为 q ,现将小球从管道内 A 处由静止释放,运动至管道内离 A 点距离为 L0的 B 点处时达到稳定速度 v0,后进入 Ⅱ 区向下偏转,从边界l2上的 D 点进入Ⅲ 区,此时速度方向与水平方向的夹角为β,最后小球恰能无碰撞的从 C处进入管道.

已知q/m=" 0" . 01C/kg, E1=" l00N" / C ,E2=E3=300N / C ,β= 600 , Bl = 103T ,L ="5m" L 0= 4m小球与管道间动摩擦因素为μ=0.1’求:
(1) 小球在管道内运动的稳定速度v0值;
(2) Ⅲ区内匀强磁场 B2的值;
(3) 从 A 处开始至从C 处进入管道的过程中,小球的运动时间t

已知q/m=" 0" . 01C/kg, E1=" l00N" / C ,E2=E3=300N / C ,β= 600 , Bl = 103T ,L ="5m" L 0= 4m小球与管道间动摩擦因素为μ=0.1’求:
(1) 小球在管道内运动的稳定速度v0值;
(2) Ⅲ区内匀强磁场 B2的值;
(3) 从 A 处开始至从C 处进入管道的过程中,小球的运动时间t
(1)1m/s(2)200T(3)9.77s
试题分析:(1)小球在从在管道中速度达到稳定时,受力平衡:
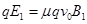 (1分)
(1分)解得:
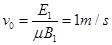 (1分)
(1分)(2)小于在从C到D的过程中,做类平抛运动,设加速度为a,在D点时竖直方向分速度为
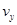 ,OD间距离为d
,OD间距离为d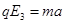 (1分)
(1分)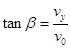 (1分)
(1分)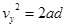 (1分)
(1分)根据题意,为保证小球恰能无碰撞的从C处进入官大,小球在三区内做匀速圆周运动的圆弧是关于CO对称的,圆心
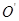 必在CO的延长线上。
必在CO的延长线上。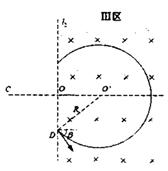
由几何关系可得:
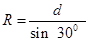
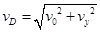 (1分)
(1分)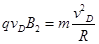 (1分)
(1分)解得:
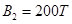 (1分)
(1分)(3)小球从A点到B的过程做变加速直线运动,设小球从A运动到B点所需要的时间为
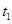 ,由牛顿第二定律得
,由牛顿第二定律得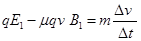 (1分)
(1分)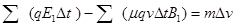 (1分)
(1分)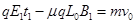 (1分)
(1分)小球从B匀速运动到C所需要的时间为
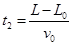 (1分)
(1分)小球在二区内运动的总时间
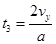 (1分)
(1分)小球在三区内运动的总时间
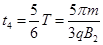 (1分)
(1分)小球从A处到C静茹管道的过程中,运动时间
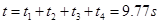 (1分)
(1分)点评:(1)对于带电粒子在复合场内运动问题首先要分清楚其运动特点和受力特点.
(2)要注意分析题目中的一些隐含条件,比如不计重力的带电粒子在正交的电场和磁场中直线运动时,一定是匀速直线运动;在混合场中做匀速圆周运动时,电场力与重力平衡.
(3)对于带电粒子在叠加场内的一般曲线运动问题(如类平抛),通常采用运动的合成与分解的方法来处理问题.还有就是要注意几何关系在解决物理问题中的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 宽为
宽为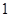 cm,
cm,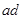 长为4cm,
长为4cm,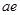 厚为
厚为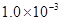 cm的导体,沿
cm的导体,沿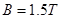 的匀强磁场垂直向里穿过
的匀强磁场垂直向里穿过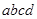 平面时,产生了
平面时,产生了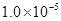 V的霍尔电压,(已知导体内定向移动的自由电荷是电子),则下列说法正确的是
V的霍尔电压,(已知导体内定向移动的自由电荷是电子),则下列说法正确的是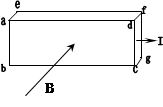
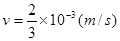
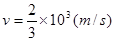
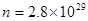 个
个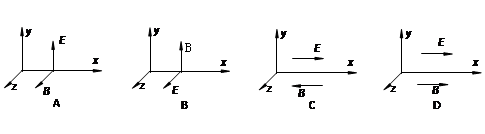
 ,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
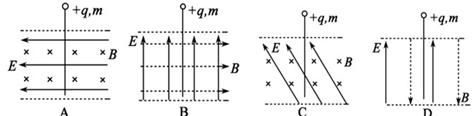

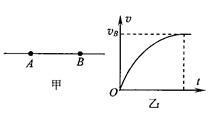
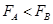
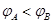
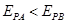
 T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求:
T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求: