题目内容
1.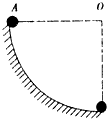 如图为一粗糙的四分之一圆弧轨道,半径为R,轨道圆心O与A点等高,一质量为m的小球在不另外施力的情况下,能以速度v沿轨道自A点匀速运动到B点,取小球在A点时为计时起点,且此时的重力势能为零,重力加速度为g,则在此过程中,下列说法正确的是( )
如图为一粗糙的四分之一圆弧轨道,半径为R,轨道圆心O与A点等高,一质量为m的小球在不另外施力的情况下,能以速度v沿轨道自A点匀速运动到B点,取小球在A点时为计时起点,且此时的重力势能为零,重力加速度为g,则在此过程中,下列说法正确的是( )| A. | 重力做功的平均功率为$\frac{1}{2}$mgv | |
| B. | 重力做的功等于小球克服摩擦力做的功 | |
| C. | 小球重力势能随时间的变化关系为Ep=mgRsin$\frac{vt}{R}$ | |
| D. | 小球的机械能随时间的变化关系为E=$\frac{1}{2}$mv2+mgRsin$\frac{vt}{R}$ |
分析 根据重力做功的大小以及运动的时间,结合平均功率的公式求出重力做功的平均功率.根据动能定理,抓住合力做功为零,得出重力做功与小球克服摩擦力做功的大小关系.根据几何关系,通过下降的高度求出重力势能的表达式,抓住机械能等于重力势能和动能之和得出机械能随时间变化的表达式.
解答 解:A、重力做功为mgR,小球运动的时间$t=\frac{\frac{πR}{2}}{v}=\frac{πR}{2v}$,则重力做功的平均功率$\overline{P}=\frac{mgR}{t}=\frac{2mgv}{π}$,故A错误.
B、小球速度大小不变,根据动能定理知,合力做功为零,由于支持力不做功,则重力做功等于小球克服摩擦力做功的大小,故B正确.
C、经过时间t,下降的高度h=Rsin$\frac{vt}{R}$,则重力势能随时间的变化关系为Ep=-mgh=-mgRsin$\frac{vt}{R}$,故C错误.
D、小球的机械能E=Ek+Ep=$\frac{1}{2}m{v}^{2}-$mgRsin$\frac{vt}{R}$,故D错误.
故选:B.
点评 解决本题的关键知道平均功率和瞬时功率的区别,掌握这两种功率的求法,以及在求解重力势能时,注意零势能平面的选取.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.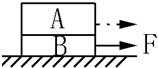 如图所示,A、B两长方体叠放在粗糙水平面上,第一次用水平恒力F1拉A,第二次用水平恒力F2拉B,都能使它们沿水平面匀速运动,而AB之间没有相对滑动,则两种情况( )
如图所示,A、B两长方体叠放在粗糙水平面上,第一次用水平恒力F1拉A,第二次用水平恒力F2拉B,都能使它们沿水平面匀速运动,而AB之间没有相对滑动,则两种情况( )
 如图所示,A、B两长方体叠放在粗糙水平面上,第一次用水平恒力F1拉A,第二次用水平恒力F2拉B,都能使它们沿水平面匀速运动,而AB之间没有相对滑动,则两种情况( )
如图所示,A、B两长方体叠放在粗糙水平面上,第一次用水平恒力F1拉A,第二次用水平恒力F2拉B,都能使它们沿水平面匀速运动,而AB之间没有相对滑动,则两种情况( )| A. | 恒力F2拉B时,A不受摩擦力作用 | B. | 恒力F1拉A时,B不受摩擦力作用 | ||
| C. | 恒力F1拉A时,A受摩擦力向左 | D. | 恒力F1大小等于F2 |
16.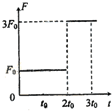 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
 质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )
质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用.力的大小F与时间t的关系如图所示,力的方向保持不变,则( )| A. | 3t0时刻的瞬时功率为$\frac{25{F}_{0}^{2}{t}_{0}}{m}$ | |
| B. | 3t0时刻的瞬时功率为$\frac{15{F}_{0}^{2}{t}_{0}}{m}$ | |
| C. | 在t=0到3t0这段时间内,水平力的平均功率为$\frac{23{F}_{0}^{2}{t}_{0}}{4m}$ | |
| D. | 在t=0到3t0这段时间内,水平力的平均功率为$\frac{25{F}_{0}^{2}{t}_{0}}{6m}$ |
6. 在如图所示的电路中,电源的电动势为E,内电阻为r.L1、L2是两个小灯泡,闭合S后,两灯均正常发光.当滑动变阻器的滑片向右滑动时,会出现( )
在如图所示的电路中,电源的电动势为E,内电阻为r.L1、L2是两个小灯泡,闭合S后,两灯均正常发光.当滑动变阻器的滑片向右滑动时,会出现( )
 在如图所示的电路中,电源的电动势为E,内电阻为r.L1、L2是两个小灯泡,闭合S后,两灯均正常发光.当滑动变阻器的滑片向右滑动时,会出现( )
在如图所示的电路中,电源的电动势为E,内电阻为r.L1、L2是两个小灯泡,闭合S后,两灯均正常发光.当滑动变阻器的滑片向右滑动时,会出现( )| A. | L1变暗 L2变暗 | B. | L1变亮 L2变暗 | C. | L1变亮 L2变亮 | D. | L1变暗 L2变亮 |
13.下列说法中正确的是( )
| A. | 只有质量和体积都极小的物体才能视为质点 | |
| B. | 路程总要大于这一段的位移大小 | |
| C. | 运动状态变化仅指速度大小的变化 | |
| D. | 重力加速度g的大小与纬度有关,赤道处g的值最小 |
11.指南针是我国古代四大发明之一.关于指南针,下列说明正确的是( )
| A. | 指南针可以仅具有一个磁极 | |
| B. | 指南针能够指向南北,说明地球具有磁场 | |
| C. | 指南针的指向不会受到附近铁块的干扰 | |
| D. | 在指南针正上方附近沿指针方向放置一直导线,导线通电时指南针不偏转 |
 如图所示,一个M=2kg的物体放在μ=0.2的粗糙水平面上,用一条质量不计的细绳绕过定滑轮和一只m0=0.1kg的小桶相连,已知:M受到的最大静摩擦力Fm=4.5N,滑轮上的摩擦不计,g=10N/kg,求在以下情况中,
如图所示,一个M=2kg的物体放在μ=0.2的粗糙水平面上,用一条质量不计的细绳绕过定滑轮和一只m0=0.1kg的小桶相连,已知:M受到的最大静摩擦力Fm=4.5N,滑轮上的摩擦不计,g=10N/kg,求在以下情况中,