题目内容
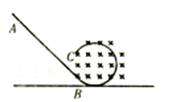
如图所示，ABC为竖直平面内的轨道，一滑块从顶点A点静止释放，沿光滑斜面AB运动的加速度为4m/s2，经过B点后，在粗糙的水平面BC上做匀减速直线运动到C点停下．已知从A点到C点所用的总时间为3s，AB段的长度为2m，设轨道经过B点拐弯处平滑连接，使得滑块经过B点前后速度的大小保持不变．求（1）滑块滑到B点时速度大小
（2）BC的长度L．
分析：根据匀变速直线运动的速度位移公式求出滑块滑到B点时的速度大小．从而根据速度时间公式求出运动到B点的时间，结合平均速度公式求出BC段的长度．
解答：解：（1）根据vB2=2asAB得，vB=
=
m/s=4m/s．
（2）从A运动到B的时间t1=
=
s=1s．
则B运动C的时间t2=3-1s=2s．
根据平均速度的公式知，L=
t2=
×2m=4m．
答：（1）滑块滑到B点的速度大小为4m/s．
（2）BC的长度L为4m．
| 2asAB |
| 2×4×2 |
（2）从A运动到B的时间t1=
| vB |
| a |
| 4 |
| 4 |
则B运动C的时间t2=3-1s=2s．
根据平均速度的公式知，L=
| vB |
| 2 |
| 4 |
| 2 |
答：（1）滑块滑到B点的速度大小为4m/s．
（2）BC的长度L为4m．
点评：解决本题的关键掌握匀变速直线运动的运动学公式和推论，并能灵活运用．
练习册系列答案
相关题目
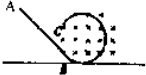如图所示，ABC为竖直平面内的光滑绝缘轨道，其中AB为倾斜直轨道，BC为与AB相切的圆形轨道，并且圆形轨道处在匀强磁场中，磁场方向垂直纸面向里．质量相同的甲、乙、丙三个小球中，甲球带正、乙球带负电、丙球不带电．现将三个小球在轨道AB上分别从不同高度处由静止释放，都恰好通过圆形轨道的最高点，则（ ）
（2012?湖南模拟）如图所示，ABC为竖直平面内的光滑绝缘轨道，其中AB为倾斜直轨道，BC为与AB相切的圆形轨道，并且圆形轨道处在匀强磁场中，磁场方向垂直纸面向里．质量相同的甲、乙、丙三个小球中，甲球带正电、乙球带负电、丙球不带电．现将三个小球在轨道AB上分别从不同高度处由静止释放，都恰好通过圆形轨道的最高点，则（ ）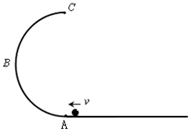
如图所示，ABC为竖直放置的半径为R=0.1m的半圆形光滑轨道，直径AC与水平面垂直，A点刚好与水平轨道相接，在轨道的最低点A安装了一个压力传感器，可测定小球在轨道内侧，通过这点时对轨道的压力F．质量为m=0.1kg的小球，以不同的初速度冲入ABC轨道．（g取10m/s2）