题目内容
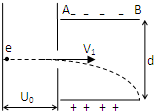
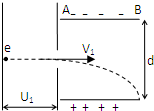 如图所示,有一初速度为零的电子(电量为e)经电压U1加速后,进入两块间距为d、电压为U2的平行金属板间.若电子从两板下中间垂直电场方向射入,且正好从下极板右边缘穿出电场,不计电子重力.
如图所示,有一初速度为零的电子(电量为e)经电压U1加速后,进入两块间距为d、电压为U2的平行金属板间.若电子从两板下中间垂直电场方向射入,且正好从下极板右边缘穿出电场,不计电子重力.求:
(1)电子被加速后进入两平行金属板的速度V1;
(2)金属板AB的长度L;
(3)电子穿出电场时的动能Ek.
分析:(1)根据动能定理求出电子加速后进入偏转电场时的速度.
(2)电子在偏转电场中做类平抛运动,根据牛顿第二定律和运动学公式,抓住等时性求出金属板AB的长度.
(3)对全过程运用动能定理,求出电子穿出电场时的动能.
(2)电子在偏转电场中做类平抛运动,根据牛顿第二定律和运动学公式,抓住等时性求出金属板AB的长度.
(3)对全过程运用动能定理,求出电子穿出电场时的动能.
解答:解:(1)电子飞离加速电场过程,由动能定理得:
eU0=
mv12
得:v1=
.
(2)电子在两板间运动时间为:t=
.
电子在偏转电场中的加速度为:a=
.
电子在偏转电场中的偏转位移为:y=
d=
at2.
解得,L=d
.
(3)由动能定理得:Ek=eU0+e
=e(U0+
).
答:(1)电子被加速后进入两平行金属板的速度v1=
.
(2)金属板AB的长度L=d
.
(3)电子穿出电场时的动能为e(U0+
).

eU0=
| 1 |
| 2 |
得:v1=
|
(2)电子在两板间运动时间为:t=
| L |
| v1 |
电子在偏转电场中的加速度为:a=
| eU |
| md |
电子在偏转电场中的偏转位移为:y=
| 1 |
| 2 |
| 1 |
| 2 |
解得,L=d
|
(3)由动能定理得:Ek=eU0+e
| U |
| 2 |
| U |
| 2 |
答:(1)电子被加速后进入两平行金属板的速度v1=
|
(2)金属板AB的长度L=d
|
(3)电子穿出电场时的动能为e(U0+
| U |
| 2 |
点评:解决本题的关键掌握类平抛运动的处理方法,将粒子的运动分解为沿电场方向和垂直电场方向,在沿电场方向上做匀加速直线运动,在垂直电场方向上做匀速直线运动,结合牛顿第二定律和运动学公式,抓住等时性进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一直升机悬停在空中向地面投放装有救灾物资的箱子,如图所示.设投放初速度为零,箱子所受的空气阻力与箱子下落速度的平方成正比,且运动过程中箱子始终保持图示姿态.在箱子下落过程中,下列说法中不正确的是( )
一直升机悬停在空中向地面投放装有救灾物资的箱子,如图所示.设投放初速度为零,箱子所受的空气阻力与箱子下落速度的平方成正比,且运动过程中箱子始终保持图示姿态.在箱子下落过程中,下列说法中不正确的是( ) (2007?攀枝花模拟)如图所示,有一箱装得很满的土豆,以一定的初速度在动摩擦因数为μ的水平地面上做匀减速运动,不计其他外力及空气阻力,则中间一质量为m的土豆A受到其他土豆对它的水平作用力大小应是( )
(2007?攀枝花模拟)如图所示,有一箱装得很满的土豆,以一定的初速度在动摩擦因数为μ的水平地面上做匀减速运动,不计其他外力及空气阻力,则中间一质量为m的土豆A受到其他土豆对它的水平作用力大小应是( )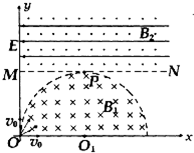 如图所示,半圆有界匀强磁场的圆心O1在x轴上,OO1距离等于半圆磁场的半径,磁感应强度大小为B1.虚线MN平行x轴且与半圆相切于P点.在MN上方是正交的匀强电场和匀强磁场,电场场强大小为E,方向沿x轴负向,磁场磁感应强度大小为B2.B1、B2方向均垂直纸面,方向如图所示.有一群相同的正粒子,以相同的速率沿不同方向从原点O射入第I象限,其中沿x轴正方向进入磁场的粒子经过P点射入MN后,恰好在正交的电磁场中做直线运动,粒子质量为m,电荷量为q (粒子重力不计).求:
如图所示,半圆有界匀强磁场的圆心O1在x轴上,OO1距离等于半圆磁场的半径,磁感应强度大小为B1.虚线MN平行x轴且与半圆相切于P点.在MN上方是正交的匀强电场和匀强磁场,电场场强大小为E,方向沿x轴负向,磁场磁感应强度大小为B2.B1、B2方向均垂直纸面,方向如图所示.有一群相同的正粒子,以相同的速率沿不同方向从原点O射入第I象限,其中沿x轴正方向进入磁场的粒子经过P点射入MN后,恰好在正交的电磁场中做直线运动,粒子质量为m,电荷量为q (粒子重力不计).求: