��Ŀ����
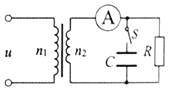
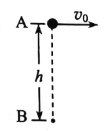
����Ŀ����ͼ������M��5kg��С�������ڹ⻬��ˮƽ���ϣ�С�����ϱ���ab��ˮƽ��a�˾���һ����m2��3kg�����P��bc��ΪR��0.5m�Ĺ⻬�ķ�֮һԲ���ι����������ˮƽ������ϸ��һ�˹̶���a�����Ϸ���O�㣬��һ��ϵ������m1��4kg��С��S����������S����ֱƽ���ڵ�A�㴦��ֹ��A����a�˵���ֱ�߶�h��2.45m���ֳ�ȥ������S�ڶ�����͵�ʱǡ��P��������������ȡ�������ٶ�g��10m/s2��
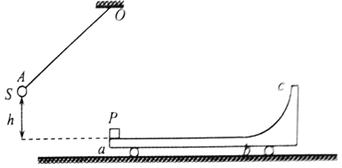
(1)������˲��P���ٶȴ�С��
(2)��ab�δֲڣ���ײ��P�����˶�ǡ����������ߵ�c����P��a�˶���c�Ĺ�������С������Ħ������������Q��
(3)��ab�ι⻬������ײ��P�˶���������c�����߶�H.
���𰸡�(1)v2��8m/s (2) Q��45J (3) H��1.5m
��������
(1)S�°ڹ��̻�е���غ㣬�ɻ�е���غ㶨�ɵã�
![]()
�������ݽ�ã�v0��7m/s
S��P����������ײ����ײ����ϵͳ�����غ㡢��е���غ㣬
������Ϊ�������ɶ����غ㶨�ɵã�
m1v0��m1v1+m2v2
�ɻ�е���غ㶨�ɵã�![]()
�������ݽ�ã�v1��1m/s��v2��8m/s��
(2)P��С����ɵ�ϵͳ��ˮƽ�������غ㣬Pǡ�õ���c��ʱ�����ٶ���ȣ�
������Ϊ��������ˮƽ�����ɶ����غ㶨�ɵã�
m2v2��(m2+M)v��
�������ݽ��:v��3m/s��
��P��С����ɵ�ϵͳ���������غ㶨�ɵ�:
![]()
�������ݽ�ã�Q��45J��
(3)P��С����ɵ�ϵͳ��ˮƽ�������غ㣬������Ϊ������
��ˮƽ�����ɶ����غ㶨�ɵã�
m2v2��(m2+M)v
�������غ㶨�ɵ�:
![]()
�������ݽ��:H��1.5m

 ��У����ϵ�д�
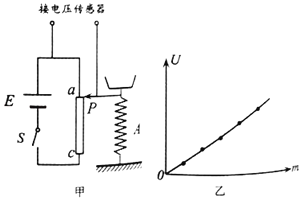
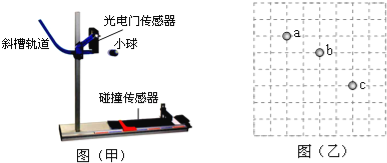
��У����ϵ�д�����Ŀ����ͼ���ף���ʾ���о�ƽ���˶����ɵ�ʵ��װ�÷�����ˮƽ�����ϣ����ù���Ŵ���������ײ���������Բ��С���ˮƽ���ٶ�v0�ͷ���ʱ��t���װ��ϵı�߿��Բ��ˮƽλ��d��
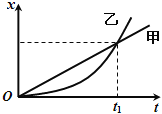
��1������б�۹����ˮƽ�ۿڸ߶�h���䣬��С���б�۵IJ�ͬ�߶ȴ����£��Բ�ͬ���ٶȳ��ˮƽ�ۿڣ�����˵����ȷ����
A����ص��ˮƽ����d����ٶ�v0������ |
B����ص��ˮƽ����d����ٶ�v0�ɷ��� |
C������ʱ��t����ٶ�v0������ |
D������ʱ��t����ٶ�v0��С�� |
��2����һλͬѧ��ʵ��ʱ����װ�õĺ�����ֱ����һ�����з���ֽ��ľ�壬Ȼ���ڷ���ֽ�ϼ�¼��С��ij��ƽ���˶�;��������λ��a��b��c��ͼ���ң���ʾ����ͬѧȡ�·���ֽ�������Ǽ�¼ˮƽ����ֱ�����ˣ���֪С����ı߳�L=1cm����С��ƽ���˶��ij��ٶȿ���Ϊ ��