题目内容
【题目】如图所示，在xOy平面内第Ⅱ象限有沿y轴负方向的匀强电场，场强大小为
N/C。y轴右侧有一个边界为圆形的匀强磁场区域，圆心O′位于x轴上，半径为r=0.02 m，磁场最左边与y轴相切于O点，磁场方向垂直纸面向里。第Ⅰ象限内与x轴相距为
m处，有一平行于x轴长为l=0.04 m的屏PQ，其左端P离y轴的距离为0.04 m。一比荷为
C/kg带正电的粒子，从电场中的M点以初速度
m/s垂直于电场方向向右射出，粒子恰能通过y轴上的N点。已知M点到y轴的距离为s=0.01 m，N点到O点的距离为
m，不计粒子的重力。求：
（1）粒子通过N点时的速度大小与方向；
（2）要使粒子打在屏上，则圆形磁场区域内磁感应强度应满足的条件；
（3）若磁场的磁感应强度为
T，且圆形磁场区域可上下移动，则粒子在磁场中运动的最长时间。
【答案】（1）
m/s，
（2）
（3）
s
【解析】试题（1）设粒子通过N点时的速度为v，速度与竖直方向的夹角为θ，粒子进入电场后做类平抛运动有：
又由牛顿第二定律有：
代入数据解得m/s
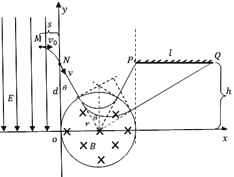
（2）由分析知粒子通过N点后将沿半径方向进入圆形磁场区域。
粒子垂直进入磁场做匀速圆周运动有：
粒子刚好打在P点时，磁感应强度最强设为
，此时粒子的轨迹半径为
由几何关系有：
代入数据解得
粒子刚好打在Q点时，磁感应强度最弱设为
，此时粒子的轨迹半径为
由几何关系有：
代入数据解得
综合得粒子要打在屏上磁感应强度满足：
（3）粒子的轨迹半径为
m
设粒子在磁场中做圆周运动的圆心角为α，弦长为
，由几何关系有：
要使粒子在磁场中运动的时间最长，则
解得
设粒子在磁场中运动的周期为T有：
s
粒子在磁场中运动的最长时间为：
s
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
