题目内容
【题目】如图所示，光滑的水平面AB 与半径
，光滑竖直半圆 轨道BCD在B点相切，D为轨道最高点。用轻质细线连接甲、乙两小球，中间夹一轻质弹簧，弹簧与甲、乙两球不拴接.甲球的质量为
，乙球的质量为
，甲、乙两球静止。现固定甲球，烧断细线，乙球离开弹簧后进入半圆轨道恰好能通过D点。重力加速度取
，甲、乙两球可看作质点。
(1)试求细线烧断前弹簧的弹性势能
；
(2)若甲球不固定，烧断细线，求从烧断细线开始到乙球脱离弹簧过程中，弹簧对乙球冲量I的大小。
【答案】（1）
（2）
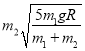
【解析】
由题意可知考查用力、能量、动量的观点分析解决问题，利用牛顿第二定律 、动量守恒定律 、能量守恒定律、动量定理计算可得。
(1)设乙球在D点处的速度为v，对乙球，在D处：
得：
(2)设甲、乙两球脱离弹簧时速度大小分别为
、
，以的方向为正方向，根据动量守恒定律得：
根据能量守恒定律得：
根据动量定理得：
冲量大小：
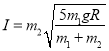
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
