题目内容
（13分）如图甲是质谱仪的工作原理示意图．图中的A容器中的正离子从狭缝S1以很小的速度进入电压为U的加速电场区(初速度不计)加速后，再通过狭缝S2从小孔G垂直于MN射入偏转磁场，该偏转磁场是以直线MN为上边界、方向垂直于纸面向外的匀强磁场，磁感应强度为B，离子最终到达MN上的H点(图中未画出)，测得G、H间的距离为d，粒子的重力可忽略不计。试求：
（1）该粒子的比荷
（2）若偏转磁场为半径为
的圆形区域，且与MN相切于G点，如图乙所示，其它条件不变，仍保证上述粒子从G点垂直于MN进入偏转磁场，最终仍然到达MN上的H点，则圆形区域中磁场的磁感应强度
与B之比为多少?
见解析
解析试题分析：（1）设离子被加速后获得的速度为v，由动能定理有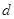
（2分）
离子在磁场中做匀速圆周运动的轨道半径 
（1分）
又 
（1分）
以上三式联立可解得 
（2分）
（2）离子在磁场中得轨迹如图所示，
（3）由几何关系有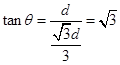
即 
（2分）
离子在磁场中做匀速圆周运动的轨道半径为
则 
（2分）
又 
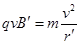（1分）
磁感应强度 （2分）
考点：动能定理，带电粒子在磁场中的运动
练习册系列答案
相关题目
m／s平抛救生圈，第一个刚落到快艇，接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇，若人的质量m，重力加速度g=10m／s2，问：
m/s沿AB方向从A点进入电场，恰好穿过孔O1和O2后，从H点离开电场。金属板间的距离L1＝2 cm，L2＝4 cm，L3＝6 cm。电子质量
kg，电荷量
C。正对的两平行板间可视为匀强电场，求：
探究能力是物理学研究的重要能力之一，物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关，为了研究砂轮的转动动能Ek与角速度ω的关系，某同学采用了下述实验方法进行探究：先让砂轮由动力带动匀速旋转，测得其角速度ω，然后让砂轮脱离动力，由于克服转轴间摩擦力做功，砂轮最后停下，测出砂轮脱离动力到停止转动的圈数n，通过分析实验数据，得出结论。经实验测得的几组ω和n如下表所示：
| ω/rad?s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek/J | | | | | |
另外已测得砂轮转轴的直径为1 cm，转轴间的摩擦力为
（1）计算出砂轮每次脱离动力的转动动能，并填入上表中。
（2）由上述数据推导出砂轮转动动能与角速度的关系式为________________。