题目内容
16.“用DIS研究加速度与力的关系”的实验装置如图(a)所示,实验中用所挂钩码的重量作为细线对小车的拉力F.通过增加钩码的数量,多次测量,可得小车运动的加速度a和所受拉力F的关系图象.他们在轨道水平和倾斜的两种情况下分别做了实验,得到了两条aF图线,如图(b)所示.
(1)图线①(选填“①”或“②”) 是在轨道右侧抬高成为斜面情况下得到的.
(2)在轨道水平时,小车运动的阻力Ff=0.5N.
(3)图(b)中,拉力F较大时,aF图线明显弯曲,产生误差,造成此误差的主要原因是C.
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.所挂钩码的总质量太大 D.所用小车的质量太大.
分析 (1)根据图象①可知,当拉力为零时,物体已经具有加速度,②图象,有拉力时,加速度为零,由此可知,一个是由于木板倾斜的太大,一个没有倾斜或者倾斜的角度太小.
(2)根据图示图象应用牛顿第二定律可以求出阻力.
(3)根据图象得出变量之间的关系,知道钩码所受的重力作为小车所受外力的条件.
解答 解:(1)在水平轨道上,由于受到摩擦力,拉力不为零时,加速度仍然为零,可知图线Ⅱ是在轨道水平的情况下得到的.当轨道的右侧抬高过高时,(平衡摩擦力过度),拉力等于0时,会出现加速度,所以图线①是在轨道右侧抬高成为斜面情况下得到的.
(2)根据牛顿第二定律得,F-f=ma,a=$\frac{F}{m}$-$\frac{f}{m}$,图线的斜率表示质量的倒数;因为F=0.5N时,加速度为零,解得f=0.5N.
(3)由牛顿第二定律可知,对M、m系统:mg=(M+m)a,对M:F=Ma,解得:F=$\frac{Mmg}{M+m}$=$\frac{mg}{1+\frac{m}{M}}$,只有当M>>m时,F≈mg,当所挂钩码的总质量m太大、不能满足条件:M>>m时,小车所受拉力明显小于mg,a-F图线明显弯曲,故C正确,故选C;
故答案为:(1)①;(2)0.5;(3)C.
点评 对于实验我们要明确实验原理、具体实验操作以及数据处理等,同时要清楚每一项操作存在的理由,只有掌握好了基本知识和基本方法才能顺利解决实验题目,所以要重视基本知识和基本方法的学习和训练.注意小车的拉力能等于重力的前提条件,并掌握图象斜率的含义.

练习册系列答案
相关题目
12.如图所示,某跳伞运动员正减速下落,下列说法正确的是( )


| A. | 伞绳对运动员的作用力小于运动员的重力 | |
| B. | 伞绳对运动员的作用力大于运动员对伞绳的作用力 | |
| C. | 运动员处于失重状态 | |
| D. | 运动员处于超重状态 |
7.真空中有两个相同的带电金属小球(可看成点电荷),带电量分别为9Q,-Q,当它们静止于空间某两点时,静电力大小为F.现用绝缘手柄将两球接触后再放回原处,则它们间静电力的大小为( )
| A. | $\frac{25}{9}F$ | B. | $\frac{9}{25}F$ | C. | $\frac{16}{9}F$ | D. | $\frac{9}{16}F$ |
4.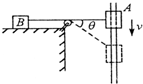 如图所示,物体A以速度v沿竖直杆匀速下滑,经细绳通过定滑轮拉动物体B在水平方向上运动,当细绳与水平方向成θ角时,物体B的运动速度为( )
如图所示,物体A以速度v沿竖直杆匀速下滑,经细绳通过定滑轮拉动物体B在水平方向上运动,当细绳与水平方向成θ角时,物体B的运动速度为( )
 如图所示,物体A以速度v沿竖直杆匀速下滑,经细绳通过定滑轮拉动物体B在水平方向上运动,当细绳与水平方向成θ角时,物体B的运动速度为( )
如图所示,物体A以速度v沿竖直杆匀速下滑,经细绳通过定滑轮拉动物体B在水平方向上运动,当细绳与水平方向成θ角时,物体B的运动速度为( )| A. | vcosθ | B. | vsinθ | C. | vtanθ | D. | vctgθ |
11.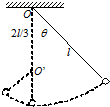 如图所示,质量为m的小球用长为l的悬绳固定于O点,在O点的正下方$\frac{2l}{3}$处有一颗钉子O′.把悬绳拉至与竖直方向成$\frac{π}{3}$弧度,然后沿切线方向以$\sqrt{2gl}$的初速度释放小球,则以下说法中正确的是( )
如图所示,质量为m的小球用长为l的悬绳固定于O点,在O点的正下方$\frac{2l}{3}$处有一颗钉子O′.把悬绳拉至与竖直方向成$\frac{π}{3}$弧度,然后沿切线方向以$\sqrt{2gl}$的初速度释放小球,则以下说法中正确的是( )
 如图所示,质量为m的小球用长为l的悬绳固定于O点,在O点的正下方$\frac{2l}{3}$处有一颗钉子O′.把悬绳拉至与竖直方向成$\frac{π}{3}$弧度,然后沿切线方向以$\sqrt{2gl}$的初速度释放小球,则以下说法中正确的是( )
如图所示,质量为m的小球用长为l的悬绳固定于O点,在O点的正下方$\frac{2l}{3}$处有一颗钉子O′.把悬绳拉至与竖直方向成$\frac{π}{3}$弧度,然后沿切线方向以$\sqrt{2gl}$的初速度释放小球,则以下说法中正确的是( )| A. | 当悬绳碰到钉子O′时,小球的速度值突然变大 | |
| B. | 当悬绳碰到钉子O′时,小球的向心加速度值突然变大 | |
| C. | 当悬绳碰到钉子O′后,小球能运动到钉子O′的正上方 | |
| D. | 当悬绳碰到钉子O′后,小球不能做半径r=$\frac{l}{3}$的圆周运动 |
1.如图所示,当开关S闭合时电磁铁和物体ab相互吸引,则正确的说法是( )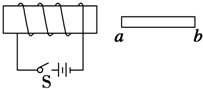

| A. | ab一定是磁铁,且a端一定是N极 | B. | ab一定是磁铁,且a端一定是S极 | ||
| C. | ab可能是磁铁,且a端是S极 | D. | ab可能是一块铁,而不是磁铁 |
5.关于摩擦力,下列说法正确的是( )
| A. | 摩擦力的方向总是和物体运动方向或运动趋势方向相反 | |
| B. | 相互接触的物体间正压力增大,摩擦力不一定增大 | |
| C. | 物体受到静摩擦力大小和接触面材料及其粗糙程度无关 | |
| D. | 运动的物体可能受到静摩擦力 |
6.自高为H的塔顶自由落下A物体的同时B物体自塔底以初速度v0竖直上抛,且A、B两物体在同一直线上运动.重力加速度为g,下面说法正确的是( )
| A. | 若v0>$\sqrt{gH}$,两物体相遇时,B正在下降途中 | |
| B. | v0=$\sqrt{gH}$,两物体在地面相遇 | |
| C. | 若$\sqrt{\frac{gH}{2}}$<v0<$\sqrt{gH}$,两物体相遇时B物正在空中下落 | |
| D. | 若v0=$\sqrt{\frac{gH}{2}}$,则两物体在地面相遇 |