题目内容
(20分)
根据玻尔理论,电子绕氢原子核运动可以看作是仅在库仑引力作用下的匀速圆周运动,已知电子的电荷量为e,质量为m,电子在第1轨道运动的半径为r1,静电力常量为k。
(1)电子绕氢原子核做圆周运动时,可等效为环形电流,试计算电子绕氢原子核在第1轨道上做圆周运动的周期及形成的等效电流的大小;
(2)氢原子在不同的能量状态,对应着电子在不同的轨道上绕核做匀速圆周运动,电子做圆周运动的轨道半径满足rn=n2r1,其中n为量子数,即轨道序号,rn为电子处于第n轨道时的轨道半径。电子在第n轨道运动时氢原子的能量En为电子动能与“电子-原子核”这个系统电势能的总和。理论证明,系统的电势能Ep和电子绕氢原子核做圆周运动的半径r存在关系:Ep=-k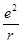 (以无穷远为电势能零点)。请根据以上条件完成下面的问题。
(以无穷远为电势能零点)。请根据以上条件完成下面的问题。
①试证明电子在第n轨道运动时氢原子的能量En和电子在第1轨道运动时氢原子的能量E1满足关系式
②假设氢原子甲核外做圆周运动的电子从第2轨道跃迁到第1轨道的过程中所释放的能量,恰好被量子数n=4的氢原子乙吸收并使其电离,即其核外在第4轨道做圆周运动的电子脱离氢原子核的作用范围。不考虑电离前后原子核的动能改变,试求氢原子乙电离后电子的动能。
(1) (2)①证明见解析;②Ek=
(2)①证明见解析;②Ek= 。
。
解析试题分析:(1)设电子绕氢原子核在第1轨道上做圆周运动的周期为T1,形成的等效电流大小为I1,根据牛顿第二定律有 (2分)
(2分)
则有  (1分)
(1分)
又因为 
 (2分)
(2分)
有  (1分)
(1分)
(2)①设电子在第1轨道上运动的速度大小为v1,根据牛顿第二定律有 (1分)
(1分)
电子在第1轨道运动的动能  (1分)
(1分)
电子在第1轨道运动时氢原子的能量 E1= -k ="-" k
="-" k (2分)
(2分)
同理,电子在第n轨道运动时氢原子的能量 En=-k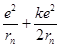 =-k
=-k (2分)
(2分)
又因为 rn=n2r1
则有 En=-k =-k
=-k
 命题得证。 (1分)
命题得证。 (1分)
② 由①可知,电子在第1轨道运动时氢原子的能量 E1=-k
电子在第2轨道运动时氢原子的能量 E2= =-k
=-k (1分)
(1分)
电子从第2轨道跃迁到第1轨道所释放的能量 ΔE= (2分)
(2分)
电子在第4轨道运动时氢原子的能量 E4= =-k
=-k (1分)
(1分)
设氢原子电离后电子具有的动能为Ek,根据能量守恒有
Ek = E4+ΔE (2分)
解得Ek=-k +
+ =
= (1分)
(1分)
说明:以上各题用其他方法解答正确均可得分。
考点:圆周运动的规律,牛顿第二定律,能量守恒定律等。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案根据牛顿第三定律,下面说法正确的是( )
| A.跳高运动员起跳时,地对人的竖直支持力大于人对地的压力 |
| B.钢丝绳吊起货物加速上升时,钢丝绳给货物的力大于货物给钢丝绳的力 |
| C.篮球场上一个小个子运动员撞在大个子运动员身上,小个子运动员跌倒了,而大个子运动员只歪了一下,是因为大个子运动员对小个子运动员作用力大于小个撞大个的力 |
| D.子弹在枪膛中加速时,枪膛对子弹的作用力等于子弹对枪膛的作用力 |
已知点电荷A的电荷量是点电荷B的2倍,则A对B的作用力大小跟B对A的作用力大小的比值为( )
| A.2∶1 | B.1∶2 | C.1∶1 | D.不能确定 |
(单选)如图所示,是某同学站在压力传感器上,做下蹲—起立的动作时记录的力随时间变化的图线。由图线可知,该同学的体重约为650 N,除此以外,还可以得到以下信息( )
| A.该同学做了两次下蹲-起立的动作 |
| B.该同学做了一次下蹲-起立的动作,且下蹲后约2 s起立 |
| C.下蹲过程中人一直处于失重状态 |
| D.下蹲过程中人先处于超重状态后处于失重状态 |
王力乘坐电梯,突然感到背上的背包变轻了,电梯此时可能在
| A.匀速上升 | B.减速下降 | C.加速上升 | D.减速上升 |
蹦极”是一项刺激的极限运动,质量为m的运动员将一端固定的长弹性绳绑在踝关节处,从几十米高处跳下。在某次蹦极中,弹性绳弹力F的大小随时间t的变化图象如图所示。将蹦极过程近似为在竖直方向的运动,弹性绳中弹力与伸长量的关系遵循胡克定律,空气阻力不计。下列说法正确的是
| A.t1~t2时间内运动员处于超重状态 |
| B.t4时刻运动员具有向上的最大速度 |
| C.t3时刻运动员的加速度为零 |
| D.t3时刻弹性绳弹力F大于2mg |
下列实例中人处于失重状态的有
| A.离开跳台后正在空中做动作的跳水运动员 |
| B.在高空匀速飞行时飞机中的乘客 |
| C.沿圆轨道运行的飞船中的宇航员 |
| D.上行电梯将要到达指定楼层时电梯中的乘客 |

