题目内容
图示为静电分选的原理示意图，将磷酸盐和石英的混合物颗粒由传送带送至两个竖直的带电平行板上方。颗粒经漏斗从电场区域中央外开始下落，经分先后的颗粒分别装入A、B两桶中，混合物离开漏斗进入电场时磷酸盐颗粒带正电，石英颗粒带负电，所有颗粒所带电量与质量之比均为10―5C/kg。若已知两板间距为d=10cm，两板的竖直高度h=50cm，设颗粒进入电场时的初速度为零，颗粒间相互作用不计。如果要使两种颗粒离开两极板间的电场区域时有最大偏转量且又恰好不接触到极板，试求：（1）两极板间所加的电压； （2）若带电平行板的下端距离A、B桶底的高度为H=1.3m，颗粒落到桶底的速度。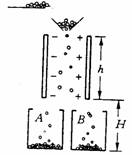
解：（1）对带电微粒进行受力分析，可得在水平方向上受电场力做匀加速直线运动，有 d/2=qUt2/2md ……………………① 在竖直方向上受重力做自由落体运动，有 h=gt2/2 ………………………………② 联立①、②解得 U=mgd2/2qh，代入数据得：U=1×104V。 （5分）（2）颗粒在下落过程中利用动能定理，有qU/2 + mg（H+h）=mvt2/2，代入数据得颗粒落至桶底的速度 vt=6m/s。 （5分）
练习册系列答案
相关题目