题目内容
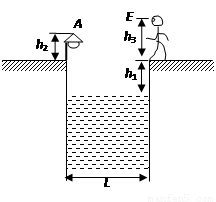
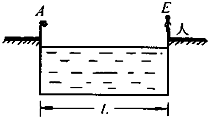
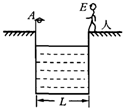如图所示，游泳池宽度L=15m，水面离岸边的高度为0.5m，在左岸边一标杆上装有一A灯，A灯距地面高0.5m，在右岸边站立着一个人，E点为人眼的位置，人眼距地面离1.5m，若此人发现A灯经水反射所成的像与左岸水面下某处的B灯经折射后所成的像重合，已知水的折射率为1.3，则B灯在水面下多深处？（B灯在图中未画出）分析：由题意根据光的折射可以作出光路图；再根据折射定律利用几何关系可得出各角之间关系，由角边关系可得出B灯的深度．
解答：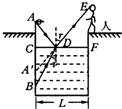
解：如图所示，设水面为CF，A到水面点C的距离为L1，B灯与水面点C之间的距离为L2，人眼到水面上点F之间的距离为L3，点C、D之间的距离为L4，由A灯光的反射得
=
，
=
得L4=5 m．
对B灯光的折射过程，有sini=sin∠CBD=
sinr=sin∠CA′D=
由
=
=
，
解得：L2=4.35m．
即B灯在水面下4.35 m深处．
答：B灯在水面下4.35 m深处．
解：如图所示，设水面为CF，A到水面点C的距离为L1，B灯与水面点C之间的距离为L2，人眼到水面上点F之间的距离为L3，点C、D之间的距离为L4，由A灯光的反射得 | L4 |
| L-L4 |
| L1 |
| L3 |
| L4 |
| 15-L4 |
| 0.5+0.5 |
| 1.5+0.5 |
得L4=5 m．
对B灯光的折射过程，有sini=sin∠CBD=
| 5 | ||
|
sinr=sin∠CA′D=
| 5 | ||
|
由
| sini |
| sinr |
| 1 |
| n |
| 1 |
| 1.3 |
解得：L2=4.35m．
即B灯在水面下4.35 m深处．
答：B灯在水面下4.35 m深处．
点评：几何光学的计算题，关键是根据题目所叙述的情景，根据几何光学的物理规律画出光路图，再根据光路图利用几何的知识分析各个线段（或角）之间的关系并利用物理规律进行运算．
练习册系列答案
相关题目
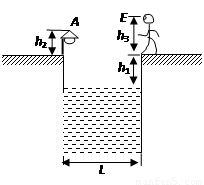
如图所示，游泳池宽度L=15m，左岸边一标杆上装有一A灯，A灯离地高0.5m，在右岸边站立着一人，E点为人眼的位置，E离地高为1.5m，水面离岸边的高度为0.5m，此人发现A灯经水面反射所成的像与左岸水面下某处的B灯经折射后所成的像重合，已知水的折射率为4/3，试求B灯在水面下多深处？（B灯在图中未画出）?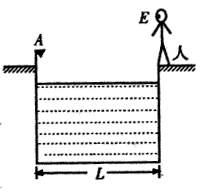
如图所示，游泳池宽度L=15m，水面离岸边的高度为0.5m，在左岸边一标杆上装有一A灯，A灯距地面高0.5m，在右岸边站立着一个人，E点为人眼的位置，人眼距地面高1.5m，若此人发现A灯经水面反射所成的像与左岸水面下某处的B灯经折射后所成的像重合，已知水的折射率为1.3，则B灯在水面下多深处？（注意：B灯在图中未画出且
到
之间都可认为等于4.35）
