题目内容
(20分)如图所示为一种获得高能粒子的装置。环形区域内存在垂直纸面向外、大小可调的匀强磁场。M、N为两块中心开有小孔的极板,每当带电粒子经过M、N板时,都会被加速,加速电压均为U;每当粒子飞离电场后,M、N板间的电势差立即变为零。粒子在电场中一次次被加速,动能不断增大,而绕行半径R不变(M、N两极板间的距离远小于R)。当t=0时,质量为m、电荷量为+q的粒子静止在M板小孔处。

(1)求粒子绕行n圈回到M板时的动能En;
(2)为使粒子始终保持在圆轨道上运动,磁场必须周期性递增,求粒子绕行第n圈时磁感应强度B的大小;
(3)求粒子绕行n圈所需总时间tn。

(1)求粒子绕行n圈回到M板时的动能En;
(2)为使粒子始终保持在圆轨道上运动,磁场必须周期性递增,求粒子绕行第n圈时磁感应强度B的大小;
(3)求粒子绕行n圈所需总时间tn。
(1)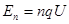 (2)
(2)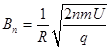 (3)
(3)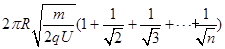
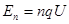 (2)
(2)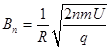 (3)
(3)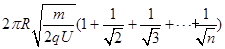
试题分析:(1)粒子绕行一圈动能的增量为
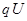 ,绕行n圈所获得的总动能
,绕行n圈所获得的总动能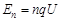 (5分)
(5分)(2)因为
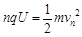 洛伦兹力提供向心力
洛伦兹力提供向心力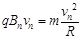
可得
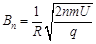 (6分)
(6分)(3)粒子做半径为R的匀速圆周运动,每一圈所用时间为
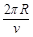 ,由于每一圈速度不同,所以每一圈所需时间也不同
,由于每一圈速度不同,所以每一圈所需时间也不同第一圈:
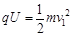
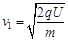
第二圈:
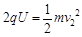
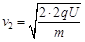
……
第n圈的速度
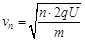 (4分)
(4分)故绕行n圈所需总时间
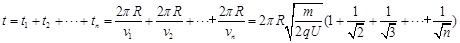 (5分)
(5分)
练习册系列答案
相关题目
 的金属小球从距水平面
的金属小球从距水平面 的光滑斜面上由静止开始释放,运动到A点时无能量损耗,水平面
的光滑斜面上由静止开始释放,运动到A点时无能量损耗,水平面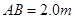 的粗糙平面, 与半径为
的粗糙平面, 与半径为 的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内, D为轨道的最高点,小球恰能通过最高点D, 完成以下要求(
的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内, D为轨道的最高点,小球恰能通过最高点D, 完成以下要求( )
)
 的值。
的值。




 =53O,具有动力装置的玩具小车质量为m=1kg,从A点开始以恒定功率P=10w由静止开始启动,运动至B点时撤去动力,小车继续沿圆弧轨道运动并冲出轨道。已知小车运动到B点时轨道对小车的支持力为FB=26
=53O,具有动力装置的玩具小车质量为m=1kg,从A点开始以恒定功率P=10w由静止开始启动,运动至B点时撤去动力,小车继续沿圆弧轨道运动并冲出轨道。已知小车运动到B点时轨道对小车的支持力为FB=26 N,小车在轨道AB上运动过程所受阻力大小恒为f=0.1mg小车可以被看成质点。取g=10m/s2,,sin53o=0.8,cos53o=0.6,求:
N,小车在轨道AB上运动过程所受阻力大小恒为f=0.1mg小车可以被看成质点。取g=10m/s2,,sin53o=0.8,cos53o=0.6,求: