题目内容
6.如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.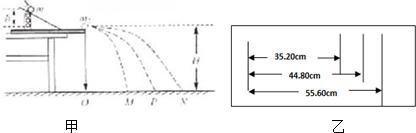
①实验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量C(填选项前的符号),间接地解决这个问题
A、小球开始释放高度h
B、小球抛出点距地面的高度H
C、小球做平抛运动的射程
②图甲中O点是小球抛出点在地面上的垂直投影,实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP,然后,把被碰小球m2静止于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.
接下来要完成的必要步骤是ADE(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM,ON
③若两球相碰前后的动量守恒,其表达式可表示为m1•OM+m2•ON=m1•OP(用②中测量的量表示);若碰撞是弹性碰撞.那么还应满足的表达式为m1•OM2+m2•ON2=m1OP2(用②中测量的量表示).
④经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图乙所示.碰撞前、后m1的动量分别为p1与p1′,则p1:p1′=14:11;若碰撞结束时m2的动量为p2′,则p1′:p2′=11:2.9.
分析 ①验证动量守恒定律实验中,质量可测而瞬时速度较难.因此采用了落地高度不变的情况下,水平射程来反映平抛的初速度大小,所以仅测量小球抛出的水平射程来间接测出速度.
②过程中小球释放高度不需要,小球抛出高度也不要求.最后可通过质量与水平射程乘积来验证动量是否守恒.
③根据碰撞前后动量守恒可以写成表达式,若碰撞为弹性碰撞,则碰撞前后动能相同.
④根据表达式将数据代入即可求出比值.
解答 解:①验证动量守恒定律实验中,即研究两个小球在轨道水平部分碰撞前后的动量关系,直接测定小球碰撞前后的速度是不容易的,根据平抛运动规律,若落地高度不变,则运动时间不变,因此可以用水平射程大小来体现速度速度大小,故需要测量水平射程,故AB错误,C正确.
②碰撞过程中动量、能量均守恒,因此有:m1v0=m1v1+m2v2
$\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}m{v}_{1}^{2}+\frac{1}{2}m{v}_{2}^{2}$,因此有:${v}_{1}=\frac{{m}_{1}-{m}_{2}}{{m}_{1}+{m}_{2}}{v}_{0}$,因此要使入射小球m1碰后不被反弹,应该满足m1>m2.
实验时,先让入射球ml多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球ml从斜轨上S位置静止释放,与小球m2相碰,并多次重复.测量平均落点的位置,找到平抛运动的水平位移,因此步骤中D、E是必须的,而且D要在E之前.至于用天平秤质量先后均可以.
故选:ADE.
③根据平抛运动可知,落地高度相同,则运动时间相同,设落地时间为t,则:
v0=$\frac{OP}{t}$,${v}_{1}=\frac{OM}{t}$,${v}_{2}=\frac{ON}{t}$,
而动量守恒的表达式是:m1v0=m1v1+m2v2
若两球相碰前后的动量守恒,则需要验证表达式m1•OM+m2•ON=m1•OP即可.
若为弹性碰撞,则碰撞前后系统动能相同,则有:
$\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}m{v}_{1}^{2}+\frac{1}{2}m{v}_{2}^{2}$,
将即满足关系式:m1•OM2+m2•ON2=m1OP2.
④碰撞前后m1动量之比:$\frac{{P}_{1}}{{P}_{1}′}=\frac{OP}{OM}=\frac{44.8}{35.2}=\frac{14}{11}$
$\frac{{P}_{1}′}{{P}_{2}′}=\frac{{m}_{1}•OM}{{m}_{2}•ON}=\frac{45.0×35.2}{7.5×55.68}=\frac{11}{2.9}$
故答案为:①C,②ADE,③m1•OM+m2•ON=m1OP,m1•OM2+m2•ON2=m1OP2④14;2.9
点评 本题考查验证动量守恒定律,在本实验中要注意学会在相同高度下,水平射程来间接测出速度,并利用动能守恒定律来解最大速度.

 阅读快车系列答案
阅读快车系列答案| A. | 1:1 | B. | 3:1 | C. | 3:4 | D. | 17:8 |
| A. | 横坐标轴x表示波的传播方向上各质点的平衡位置 | |
| B. | 横坐标轴x表示质点距波源的距离 | |
| C. | 纵坐标轴y表示某一时刻各个质点偏离平衡位置的位移 | |
| D. | 坐标原点一定是波源的位置 |
 图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则( )
图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则( )| A. | 该波沿x轴负方向传播 | |
| B. | 该波沿x轴正方向传播 | |
| C. | t=0.15s时,质点Q的加速度达到正向最大 | |
| D. | t=0.15s时,质点P的运动方向沿y轴正方向 | |
| E. | 从t=0.10到t=0.25s,质点P通过的路程小于30cm |
 粗糙的地面上放着一个质量M=1.5kg的斜面,斜边部分光滑,底面与地面的动摩擦因数μ=0.2,倾角θ=37°,在固定在斜面的挡板上用轻质弹簧连接一质量m=0.5kg 的小球,弹簧劲度系数k=200N/m,现给斜面施加一水平向右为F的恒力作用,使整体向右以a=1m/s2匀加速运动.
粗糙的地面上放着一个质量M=1.5kg的斜面,斜边部分光滑,底面与地面的动摩擦因数μ=0.2,倾角θ=37°,在固定在斜面的挡板上用轻质弹簧连接一质量m=0.5kg 的小球,弹簧劲度系数k=200N/m,现给斜面施加一水平向右为F的恒力作用,使整体向右以a=1m/s2匀加速运动. 用螺旋测微器测量某金属丝的直径,测量读数为0.605mm,则此时测微器的可动刻度上的A、B、C刻度线(见图)所对应的刻度值依次是15、10、5.
用螺旋测微器测量某金属丝的直径,测量读数为0.605mm,则此时测微器的可动刻度上的A、B、C刻度线(见图)所对应的刻度值依次是15、10、5.