题目内容
17. 如图所示,不计空气阻力.长为1m细绳一端固定在天花板上,另一端拴一质量为2kg的小球,当小球以4m/s速度摆到最低点时,绳子的拉力为多少?(取重力加速度g=10m/s2)
如图所示,不计空气阻力.长为1m细绳一端固定在天花板上,另一端拴一质量为2kg的小球,当小球以4m/s速度摆到最低点时,绳子的拉力为多少?(取重力加速度g=10m/s2)
分析 小球通过最低点时由重力和绳子的拉力的合力提供向心力,根据牛顿第二定律求解.
解答 解:在最低点,根据牛顿第二定律得:
T-mg=m$\frac{{v}^{2}}{l}$
解得:T=20+3×$\frac{16}{1}$=68N
答:绳子的拉力为68N.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
12.质量相同的氢气和氧气,温度相同,如果气体分子势能忽略不计,则( )
| A. | 氧气的内能较大 | |
| B. | 氢气的内能较大 | |
| C. | 氢气分子的平均动能和氧气分子的平均动能相同 | |
| D. | 氢气分子的平均速率和氧气分子的平均速率相同 |
7.一滑块以某一速度从斜面底端滑到顶端时,其速度恰好减为零,若设斜面全长为L,滑块通过最初$\frac{3}{4}$L所需时间为t,则滑块从斜面底端到斜面顶端全过程的平均速度为( )
| A. | $\frac{3L}{4t}$ | B. | $\frac{L}{t}$ | C. | $\frac{L}{2t}$ | D. | 2t |
 如图所示,一台模型发电机的电枢是矩形导线框abcd,其ab和bc边长均为0.2m,匝数N=100,它在磁感应强度B=0.2T的匀强磁场中,绕通过线框对称中心且垂直于磁场方向的轴OO′匀速转动,并通过滑环和电刷与外电路连接,当S断开时,交流电压表示数为10$\sqrt{2}$V,当S闭合时,标有“10V 10W”的灯泡恰好正常发光,求:
如图所示,一台模型发电机的电枢是矩形导线框abcd,其ab和bc边长均为0.2m,匝数N=100,它在磁感应强度B=0.2T的匀强磁场中,绕通过线框对称中心且垂直于磁场方向的轴OO′匀速转动,并通过滑环和电刷与外电路连接,当S断开时,交流电压表示数为10$\sqrt{2}$V,当S闭合时,标有“10V 10W”的灯泡恰好正常发光,求:
 为了测定滑块与桌面之间的动摩擦因数,某同学设计了如图所示的实验装置.其中,a是质量为m的滑块(可视为质点),b是可以固定于桌面的滑槽(滑槽末端与桌面相切).第一次实验时,将滑槽固定于水平桌面的右端,滑槽的末端与桌面的右端M对齐,让滑块a从滑槽上最高点由静止释放滑下,落在水平地面上的P点;第二次实验时,将滑槽固定于水平桌面的左端,测出滑槽的末端N 与桌面的右端M的距离为L,让滑块a再次从滑槽上最高点由静止释放滑下,落在水平地面上的P′点.已知当地重力加速度为g,不计空气阻力.
为了测定滑块与桌面之间的动摩擦因数,某同学设计了如图所示的实验装置.其中,a是质量为m的滑块(可视为质点),b是可以固定于桌面的滑槽(滑槽末端与桌面相切).第一次实验时,将滑槽固定于水平桌面的右端,滑槽的末端与桌面的右端M对齐,让滑块a从滑槽上最高点由静止释放滑下,落在水平地面上的P点;第二次实验时,将滑槽固定于水平桌面的左端,测出滑槽的末端N 与桌面的右端M的距离为L,让滑块a再次从滑槽上最高点由静止释放滑下,落在水平地面上的P′点.已知当地重力加速度为g,不计空气阻力.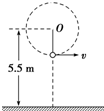 如图所示,一质量为m=2kg的小球用细绳拴住在竖直平面内做圆周运动,绳长L=0.5m,固定点O距地面的高度为5.5m,绳的最大承受力F=120N,则:
如图所示,一质量为m=2kg的小球用细绳拴住在竖直平面内做圆周运动,绳长L=0.5m,固定点O距地面的高度为5.5m,绳的最大承受力F=120N,则: 如图所示,光滑水平地面上停放着一辆质量为M的小车,小车的左侧靠在竖直墙壁上,半径为R的四分之一光滑圆弧轨道AB的最低点B与水平轨道BD平滑相接,车的右端固定有一个轻质弹簧,水平轨道BC段粗糙,CD段光滑.现有一可视为质点的质量为m物块从A点正上方h=2R处无初速度下落,恰好落入小车沿圆轨道滑动,然后沿水平轨道滑行,与弹簧相接触并压缩弹簧,弹簧原长时左端处于C点,始终处于弹性限度内,最后又返回到B相对于车静止.已知M=5m,物块与水平轨道BC间的动摩擦因数为μ,不考虑空气阻力和物块落入圆弧轨道时的能量损失.求
如图所示,光滑水平地面上停放着一辆质量为M的小车,小车的左侧靠在竖直墙壁上,半径为R的四分之一光滑圆弧轨道AB的最低点B与水平轨道BD平滑相接,车的右端固定有一个轻质弹簧,水平轨道BC段粗糙,CD段光滑.现有一可视为质点的质量为m物块从A点正上方h=2R处无初速度下落,恰好落入小车沿圆轨道滑动,然后沿水平轨道滑行,与弹簧相接触并压缩弹簧,弹簧原长时左端处于C点,始终处于弹性限度内,最后又返回到B相对于车静止.已知M=5m,物块与水平轨道BC间的动摩擦因数为μ,不考虑空气阻力和物块落入圆弧轨道时的能量损失.求