题目内容
20. 一列横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.05s时刻的波形图.求:
一列横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.05s时刻的波形图.求:(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
(3)若T<t2-t1,并且波速为360m/s,则波沿哪个方向传播?
分析 (1)由于题中没有给出波的传播方向,故需要对波沿x轴正方向和x轴负方向传播分别进行讨论.又因为题中没有给出△t=t2-t1与周期T的关系,故需要考虑到波的周期性.运用波形平移法得出波的传播距离s与波长的关系,由v=$\frac{S}{t}$求得波速的两个通项.
(2)波的一个周期内传播的距离是λ,当2T>t2-t1>T时,可知2λ>S>λ,根据上题结果分析求解本题.
(3)根据时间和波速,由S=vt求出波传播的距离,利用波形的平移法判断波的传播方向.
解答 解:(1)因为题中没有给出波的传播方向,故需要对波沿x轴正方向和x轴负方向传播分别进行讨论.又因为题中没有给出△t=t2-t1与周期T的关系,故需要考虑到波的重复性.
若波沿x轴正方向传播,则可看出是波形传播的最小距离 S0=$\frac{1}{4}$λ=2m
波传播的可能距离是 S=S0+nλ=8n+2(m)
则可能的波速为 v=$\frac{S}{t}$=$\frac{8n+2}{0.05}$=160n+40(m/s),(n=0、1、2、…,)
若波沿x轴负方向传播,则可看出是波形传播的最小距离 S0=$\frac{3}{4}$λ=6m
波传播的可能距离是 S=S0+nλ=8n+6(m)
则可能的波速为 v=$\frac{S}{t}$=160n+120(m/s),(n=0、1、2、…,)
(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>S>λ,这时波速的通解表达式中n=1.代入上题结果得:
若波沿x轴正方向传播,则波速为 v=200(m/s)
若波沿x轴负方向传播,则波速为 v=280m/s( m/s)
(3)当T<t2-t1,波速为360m/s时,根据波动与振动的对应性可知 t2-t1>T,所以波向前传播的距离大于波长S>λ,而且可以计算出 S=vt=360×0.05m=18m
由于波长等于8m,这样波向前传播了 $\frac{S}{λ}$=$\frac{18}{8}$=2$\frac{1}{4}$λ.由波形图不难判断出波是沿x轴向右传播的.
也可以由波速的通解表达式来判断:
若波沿x轴正方向传播,则波速为 v=160n+40(m/s),当n=2时,v=360(m/s).
若波沿x轴负方向传播,则波速为 v=160n+120(m/s),当n=1时,v=280( m/s),当n=2时,v=440(m/s).
所以波是沿x轴向右传播的.
答:
(1)波速是(160n+40)m/s或(160n+120)m/s,(n=0、1、2、…,);
(2)若2T>t2-t1>T,波速又为200m/s或280m/s.
(3)若T<t2-t1,并且波速为360m/s,则波向右传播.
点评 本题关键抓住波的周期性和双向性,运用波形的平移法进行分析和求解,是典型的多解问题,要防止漏解.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 光的干涉和衍射不仅说明了光具有波动性,还说明了光是横波 | |
| B. | 全息照片往往用激光来拍摄,主要是利用光的干涉来实现的 | |
| C. | 验钞机是利用红外线的特性工作的 | |
| D. | 拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 |

| A. | b光的频率比c光小 | |
| B. | 在真空中,a光传播速度比b、c大 | |
| C. | 在玻璃砖中,a光传播速度比b、c小 | |
| D. | a光的光子能量最小 | |
| E. | 若以a、b、c三种单色光分别用相同的装置做“用双缝干涉测定单色光的波长”的实验,则a光观察到的条纹间距最大 |
| A. | 如果物体(或系统)所受到的合外力为零,则机械能一定守恒 | |
| B. | 如果合外力对物体(或系统)做功为零,则机械能一定守恒 | |
| C. | 物体沿固定光滑曲面自由下滑过程中,不计空气阻力,机械能一定守恒 | |
| D. | 做匀加速运动的物体,其机械能可能守恒 |
 如图,为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样,每列波振幅均为A,其中实线表示波峰,虚线表示波谷,则关于介质中的a、b、c、d四点,(b、c为相邻波峰和波谷的中点)下列说法正确的是( )
如图,为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样,每列波振幅均为A,其中实线表示波峰,虚线表示波谷,则关于介质中的a、b、c、d四点,(b、c为相邻波峰和波谷的中点)下列说法正确的是( )| A. | a、c振幅为2A,b、d始终不动 | |
| B. | 图示时刻d点位移大小为2A,b、c、d三点位移为零 | |
| C. | a点位移大小始终为2A,d点位移始终为零 | |
| D. | 这四个点全部是振动减弱点 |
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示.下列说法中正确的是( )| A. | 图线1表示竖直分运动的v-t图线 | B. | 图线2表示水平分运动的v-t图线 | ||
| C. | 图线1表示水平分运动的v-t图线 | D. | 以上说法都不对 |
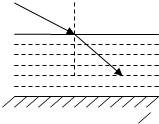 如图所示,某透明液体深1m,一束与水平面成30°角的光线,从空气照向该液体,进入该液体的光线与水平面的夹角为60°.(已知光在真空中的光速为C).试求:
如图所示,某透明液体深1m,一束与水平面成30°角的光线,从空气照向该液体,进入该液体的光线与水平面的夹角为60°.(已知光在真空中的光速为C).试求: