题目内容
某消防队员在一次执行任务过程中,遇到突发事件,需从10m长的直杆顶端从静止开始匀加速下滑,加速度大小a1=8m/s2,然后立即匀减速下滑,减速时的最大加速度a2=4m/s2,若落地时的速度不允许超过4m/s,把消防队员看成质点,求该队员下滑全过程的最短时间.
解:设匀加速直线运动的最大速度为v,则匀加速直线运动的位移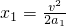 =
=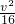
匀减速直线运动的位移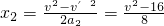
因为x1+x2=10m
解得v=8m/s.
则匀加速直线运动的时间
匀减速直线运动的时间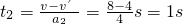
所以t=1+1s=2s.
答:该队员下滑全过程的最短时间为2s.
分析:设匀加速直线运动的最大速度为v,根据速度位移公式求出匀加速直线运动和匀减速直线运动的位移,抓住两者之和等于10m,求出匀加速直线运动的最大速度,再根据速度时间公式求出两段过程的时间,从而求出下滑全过程的最短时间.
点评:解决本题的关键掌握匀变速直线运动的速度位移公式 以及速度时间公式v=v0+at.
以及速度时间公式v=v0+at.
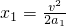 =
=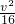
匀减速直线运动的位移
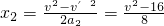
因为x1+x2=10m
解得v=8m/s.
则匀加速直线运动的时间

匀减速直线运动的时间
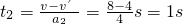
所以t=1+1s=2s.
答:该队员下滑全过程的最短时间为2s.
分析:设匀加速直线运动的最大速度为v,根据速度位移公式求出匀加速直线运动和匀减速直线运动的位移,抓住两者之和等于10m,求出匀加速直线运动的最大速度,再根据速度时间公式求出两段过程的时间,从而求出下滑全过程的最短时间.
点评:解决本题的关键掌握匀变速直线运动的速度位移公式
 以及速度时间公式v=v0+at.
以及速度时间公式v=v0+at. 
练习册系列答案
相关题目