题目内容
18.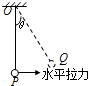 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点.不计空气阻力.
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点.不计空气阻力.(1)用水平拉力将小球从平衡位置P点很缓慢地移动到Q点,此时轻绳与竖直方向的夹角为θ,求拉力做的功.
(2)在Q点撤去拉力,让小球从静止开始下摆,求小球经过P点时的速度.
分析 (1)将小球从P点缓慢移动到Q点,动能的变化量为零,结合动能定理求出拉力做功的大小.
(2)根据动能定理求出小球静止释放后经过P点的速度.
解答 解:(1)根据动能定理得,WF-mgL(1-cosθ)=0,
解得WF=mgL(1-cosθ).
(2)撤去拉力,根据动能定理得,$mgL(1-cosθ)=\frac{1}{2}m{v}^{2}$,
解得v=$\sqrt{2gL(1-cosθ)}$.
答:(1)拉力做功为mgL(1-cosθ).
(2)小球经过P点的速度为$\sqrt{2gL(1-cosθ)}$.
点评 本题考查了动能定理的基本运用,运用动能定理解题,关键选择好研究的过程,分析过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
8.热现象过程中不可避免地出现能量耗散现象.所谓能量耗散是指在能量转化过程中无法把流散的能量重新收集、重新加以利用.下列关于能量耗散的说法中正确的是( )
| A. | 能量耗散说明能量不守恒 | |
| B. | 能量耗散不符合客观规律 | |
| C. | 能量耗散过程中能量仍守恒,只是能量的转化有方向性 | |
| D. | 待科技发达到一定程度可消除能量耗散现象,实现永动机 |
6.在下列实例中,不计空气阻力,机械能守恒的是( )
| A. | 沿竖直方向自由下落的物体 | B. | 做竖直上抛运动的物体 | ||
| C. | 起重机将重物体匀速吊起 | D. | 沿光滑竖直圆轨道运动的小球 |
10.下面关于万有引力的说法中正确的是( )
| A. | 万有引力是普遍存在于宇宙中所有具有质量的物体之间的相互作用 | |
| B. | 重力和万有引力是两种不同性质的力 | |
| C. | 地球对苹果的引力大于苹果对地球的引力 | |
| D. | 当两物体间距为零时,万有引力将无穷大 |
8.下面关于交变电流的说法中正确的是( )
| A. | 交流电器设备上所标的电压和电流值是交变电流的最大值 | |
| B. | 用交流电表测定的读数值是交流电的瞬时值 | |
| C. | 给定的交变电流数值,在没有特别说明的情况下都是指瞬时值 | |
| D. | 跟交变电流有相同热效应的直流电的数值是交变电流的有效值 |
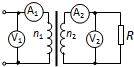 如图所示,理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,交变电源的电动势e=311sin314tV,电阻R=88Ω,电流表和电压表对电路的影响忽略不计.则电压表V1的示数为220V,电流表A1的示数为0.1A,电流表A2的示数为0.5A.
如图所示,理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,交变电源的电动势e=311sin314tV,电阻R=88Ω,电流表和电压表对电路的影响忽略不计.则电压表V1的示数为220V,电流表A1的示数为0.1A,电流表A2的示数为0.5A.