题目内容
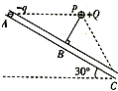
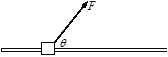
【题目】如图,将质量m=0.1kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径。环与杆间动摩擦因数![]() =0.8。对环施加一位于竖直平面内斜向上,与杆夹角
=0.8。对环施加一位于竖直平面内斜向上,与杆夹角![]() =530的拉力F,使圆环以a=4.4m/s2的加速度沿杆运动,则F的大小可能为(取sin530=0.8,cos530=0.6,g=10m/s2)( )
=530的拉力F,使圆环以a=4.4m/s2的加速度沿杆运动,则F的大小可能为(取sin530=0.8,cos530=0.6,g=10m/s2)( )
A.1N B.3 N C.7N D.9N
【答案】AD
【解析】
试题分析:对环受力分析,受重力、拉力、弹力和摩擦力;令![]() ,F=1.25N此时无摩擦力。
,F=1.25N此时无摩擦力。
圆环沿杆做匀加速运动
当F<1.25N时,杆对环的弹力向上,由牛顿第二定律有:
水平方向上:![]()
竖直方向上:![]()
解得:F=1N
当F>1.25N时,杆对环的弹力向下,有由牛顿第二定律有:
水平方向:![]()
竖直方向:![]()
解得:F=9N
故AD对。
考点: 牛顿第二定律的综合运用。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】某同学在“研究匀变速直线运动”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻两点间的距离如图甲所示,每两个相邻的计数点之间的时间间隔均为0.10s。
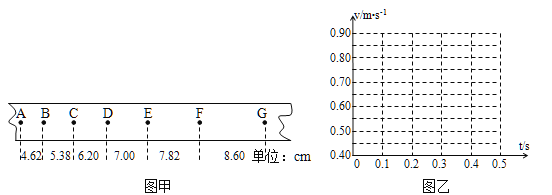
(1)试根据纸带上各个计数点间的距离,计算打下B、C、D、E、F五个点时小车的瞬时速度,请将D点的速度值填在下面的表格内(保留到小数点后两位);
计数点序号 | B | C | D | E | F |
计数点对应的时刻t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
通过计数点时小车的速度v/ms﹣1 | 0.50 | 0.58 | 0.74 | 0.82 |
(2)以A点为计时零点,将B、C、D、E、F各个时刻的瞬时速度标在如图乙所示的坐标纸上,并画出小车的瞬时速度v随时间t变化的关系图线;
(3)根据第(2)问中画出的v﹣t图线,求出小车运动的加速度大小a= m/s2(保留三位有效数字)。