题目内容
11.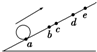 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=$\sqrt{8}$m/s | B. | vc=1.5m/s | ||
| C. | xde=3m | D. | 从d到e所用时间为4s |
分析 由题,小球从a到c和从c到d所用的时间都是2s,则根据推论得知,c点的速度等于ad间的平均速度,并利用推论求出ac间和cd间中点时刻的瞬时速度,即可求出加速度,再由位移公式求出b点的速度,由速度公式求出从d到e所用时间.
解答 解:A、由题,小球从a到c和从c到d所用的时间都是2s,根据推论得知,c点的速度等于ad间的平均速度,则有:
${v}_{c}=\frac{ac+cd}{2t}=\frac{12}{2×2}m/s=3m/s$,
ac间中点时刻的瞬时速度为:${v}_{1}=\frac{ac}{t}=\frac{7}{2}m/s=3.5m/s$,
cd间中点时刻的瞬时速度为:${v}_{2}=\frac{cd}{t}=\frac{5}{2}m/s=2.5m/s$,
故物体的加速度大小为:a=$\frac{{v}_{2}-{v}_{1}}{t}=0.5m/{s}^{2}$,
由${{v}_{b}}^{2}-{{v}_{c}}^{2}=2a•bc$,代入数据解得${v}_{b}=\sqrt{10}m/s$,故A、B错误.
C、设c点到最高点的距离为S,则:$s=\frac{{{v}_{c}}^{2}}{2a}=\frac{9}{2×0.5}m=9m$,则de=S-cd=9m-5m=4m.故C错误.
D、设d到e的时间为T,则de=$\frac{1}{2}a{T}^{2}$,代入数据解得T=4s,故D正确.
故选:D.
点评 本题对运动学公式要求较高,要求学生对所有的运动学公式不仅要熟悉而且要熟练,要灵活,基本方法就是平时多练并且尽可能尝试一题多解.

练习册系列答案
相关题目
19.某人造卫星绕地球做匀速圆周运动,设地球半径为R,地面重力加速度为g,下列说法错误的是( )
| A. | 人造卫星的最小周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 卫星在距地面高度R处的绕行速度为$\sqrt{\frac{Rg}{2}}$ | |
| C. | 卫星在距地面高度为R处的加速度为$\frac{g}{4}$ | |
| D. | 地球同步卫星的速率比近地卫星速率小,所以发射同步卫星的发射速度较小 |
6.在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示.产生的交变电动势随时间变化的规律如图乙所示.则下列说法正确的是( )


| A. | t=0.01s时矩形金属线框平面与磁感线平行 | |
| B. | 该线圈1s转过100圈 | |
| C. | 该交变电动势的周期为2s | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
16.物体做曲线运动时,下列说法中正确的是( )
| A. | 速度一定变化 | |
| B. | 加速度一定变化 | |
| C. | 合力一定不为零 | |
| D. | 合力方向与速度方向可能在同一直线上 |
3.下列说法正确的是( )
| A. | 牛顿发现了万有引力定律,并测出了引力常量 | |
| B. | 安培发现了电流的磁效应,洛伦兹通过实验测定了磁场对电流的作用力 | |
| C. | 静止导线中通稳恒电流也可以在近旁的静止线圈中感应出电流 | |
| D. | 伽利略科学思想的核心是把科学实验和逻辑推理有机结合起来 |
20.一小球做平抛运动,t秒末速度与水平方向成θ1角,t+t0时刻速度与水平方向成θ2角,不计空气阻力,重力加速度为g,则小球初速度大小为( )
| A. | $\frac{g{t}_{0}}{tan{θ}_{2}-tan{θ}_{1}}$ | B. | $\frac{g{t}_{0}}{tan{θ}_{2}+tan{θ}_{1}}$ | ||
| C. | gt0(cosθ1-cosθ2) | D. | gt0(tanθ2-tanθ1) |
1. 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )| A. | 霍尔元件能够把电学量转换为磁学量的传感器 | |
| B. | 若霍尔元件的载流子是自由电子,则电势差UMN<0 | |
| C. | 仅增大磁感应强度时,电势差UMN变大 | |
| D. | 在测定地球赤道上方的地磁场强弱时,元件的工作面应保持水平 |