题目内容
【题目】如图所示，穿有M、N两个小球(均视为质点)的光滑绝缘圆环，固定在竖直面内，圆心为O、半径为R=0.3 m。M、N用一根不可伸长的绝缘轻质细绳相连，质量分别为mM=0.01 kg、mN=0.08kg；M带电量q=+7×10-4C，N不带电。该空间同时存在匀强电场和匀强磁场。电场方向竖直向上，电场强度E=1×103V／m；磁场方向垂直于圆环平面向里，磁感应强度B=
×102 T。将两小球从图示位置(M与圆心O等高，N在圆心O的正下方)由静止释放，两小球开始沿逆时针向上转动。取重力加速度g=10m／s2，已知sin37°=0.6，cos37°=0.8。则在两球从图示位置逆时针向上转动的过程中，求：
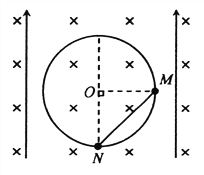
(1)通过计算判断，小球M能否到达圆环的最高点?
(2)小球M速度最大时，圆环对小球M的弹力。
(3)小球M电势能变化量的最大值。
【答案】（1）M不能到达圆环最高点 （2）-0.096N （3） 0.2016J
【解析】 （1）设MN在转动过程中，绳对MN做的功分别为Wr、
,则
设M到达圆环最高点时，MN的动能分别为EKM、EKN
对M，洛伦兹力不做功，由动能定理可得：
对N由动能定理：
联立解得：
即：M在圆环最高点时，系统动能为负值；故M不能到达圆环最高点。
（2）设N转过α角时，MN的速度大小分别为vM、vN，因MN做圆周运动的半径和角速度均相同，则vM=vN
对M，洛伦兹力不做功，根据动能定理
对N由动能定理：
联立解得：
由上式可知，当
时，MN达到最大速度，最大速度为
M速度最大时，设绳子拉力为F，圆环对小球M的弹力FN,
由牛顿运动定律
解得：FN=-0.096N 负号表示弹力方向沿圆环径向向外
（3）MN从图示位置逆时针转动过程中，由于M不能到达最高点，所以，当两球速度为零时，电场力做功最多，电势能减小最多，由可得：
=0
解得：
或
故M的电势能减小量的最大值为：
