题目内容
【题目】如图，POQ是折成600角的固定于竖直平面内的光滑金属导轨，导轨关于竖直轴线对称， 
，整个装置处在垂直导轨平面向里的足够大的匀强磁场中，磁感应强度随时间变化规律为B=1-8t(T)。一质量为1kg、长为L、电阻为
、粗细均匀的导体棒锁定于OP、OQ的中点a、b位置．当磁感应强度变为B1=0.5T后保持不变，同时将导体棒解除锁定，导体棒向下运动，离开导轨时的速度为v=3.6m/s。导体棒与导轨始终保持良好接触，导轨电阻不计，重力加速度为g=10m/s2下列说法正确的是
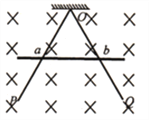
A. 导体棒解除锁定前回路中电流的方向是aboa
B. 导体棒解除锁定前回路中电流大小是
C. 导体棒滑到导轨末端时的加速度大小是7.3m/s2
D. 导体棒运动过程中产生的焦耳热是2.02J
【答案】BC
【解析】试题分析：根据法拉第电磁感应定律列式求解感应电动势大小，根据欧姆定律求解感应电流大小，根据楞次定律和安培定则判断感应电流的方向；根据切割公式求解感应电动势，根据欧姆定律求解感应电流，根据安培力公式求解安培力，根据牛顿第二定律列式求解加速度；根据能量守恒定律列式求解运动过程中产生的焦耳热．
解除锁定前，感应电动势为：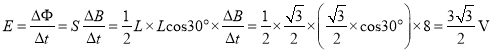 
；感应电流为
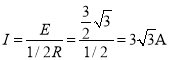，由楞次定律知，感应电流的方向为顺时针方向，A错误B正确；滑到导轨末端时的，感应电动势为
，感应电流为： 
，安培力为
；根据牛顿第二定律，有： 
，解得
，C正确；由能量守恒得
，解得
，D错误．
练习册系列答案
轻松暑假总复习系列答案
相关题目
