题目内容
18.某同学利用图所示的实验装置,探究物块在水平桌面上的运动规律.物块在重物的牵引下开始运动,重物落地后,物块再运动一段距离停在桌面上(尚未到达滑轮处).从纸带上便于测量的点开始选取计数点(每相邻两个计数点之间有4个点未画出),相邻两个计数点之间的时间间隔记为T,邻计数点间的距离如图所示.打点计时器电源的频率为f=50Hz.
(1)通过分析纸带数据,可判断物块在两相邻计数点6和7之间某时刻开始减速.
(2)计数点5对应的速度大小为1.00m/s(保留两位有效数字)
(3)计算物块在减速阶段的加速度a=-2.00m/s2.(结果保留两位有效数字)
(4)物块在加速时,其加速度的方向是:“5到1”(选填“l到5”或者“5到1”)
分析 (1)根据相等时间内位移逐渐减小,判断从哪两个计数点之间开始减速.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点5的瞬时速度.
(3)根据连续相等时间内的位移之差是一恒量求出减速的加速度.
(4)加速时加速度的方向与速度方向相同,根据速度方向确定加速度的方向.
解答 解:(1)从纸带上的数据分析得知:在点计数点6之前,两点之间的位移逐渐增大,是加速运动,在计数点7之后,两点之间的位移逐渐减小,是减速运动,所以物块在相邻计数点6和7之间某时刻开始减速;
(2)计数点5的瞬时速度${v}_{5}=\frac{{s}_{4}+{s}_{5}}{2T}=\frac{(9.00+11.01)×1{0}^{-2}}{0.2}$m/s≈1.00m/s.
(3)对于减速阶段,根据△x=aT2,运用逐差法得,$a=\frac{{s}_{9}+{s}_{10}-{s}_{7}-{s}_{8}}{4{T}^{2}}$=$\frac{(4.60+6.60-8.61-10.60)×1{0}^{-2}}{4×0.01}$=-2.00m/s2.
(4)加速阶段,加速度的方向与速度方向相同,可知加速度方向由“5到1”.
故答案为:(1)6,7,(2)1.00,(3)-2.00,(4)“5到1”.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.一质点做匀加速直线运动,通过第一段8m位移所用的时间为2s,紧接着通过下一段10m位移所用时间为1s.则该质点运动的加速度大小为( )
| A. | 4m/s2 | B. | 5m/s2 | C. | 6m/s2 | D. | 7m/s2 |
13.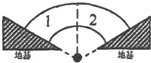 将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
 将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
7.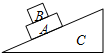 物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.当两者以相同的初速度沿固定斜面C向下做匀速运动时,( )
物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.当两者以相同的初速度沿固定斜面C向下做匀速运动时,( )
 物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.当两者以相同的初速度沿固定斜面C向下做匀速运动时,( )
物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.当两者以相同的初速度沿固定斜面C向下做匀速运动时,( )| A. | A受到B的摩擦力沿斜面方向向上 | |
| B. | A受到B的摩擦力沿斜面方向向下 | |
| C. | A受到斜面的摩擦力为零 | |
| D. | A受到斜面的摩擦力沿斜面方向向上 |
8.两辆相同的汽车,一辆空载,一辆满载,在同一水平公路路面上直线行驶,下面关于两车车速、动能、惯性、质量和滑行路程的讨论,正确的是( )
| A. | 车速较大的汽车,它的惯性较大 | |
| B. | 动能较大的汽车,它的惯性较大 | |
| C. | 行驶速度相同时,质量较大的汽车,刹车后滑行的路程较长 | |
| D. | 以额定功率匀速行驶时,质量较小的汽车,刹车后滑行的路程较长 |
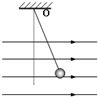 用长为L的细线将质量为m的带电小球悬挂在O点,且O点距水平地面的高度为h,当空间中有水平向右电场强度为E的匀强电场(假设地面上方的匀强电场范围足够大)时,细线偏转α角度后处于静止状态,重力加速度为g.
用长为L的细线将质量为m的带电小球悬挂在O点,且O点距水平地面的高度为h,当空间中有水平向右电场强度为E的匀强电场(假设地面上方的匀强电场范围足够大)时,细线偏转α角度后处于静止状态,重力加速度为g.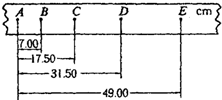 在研究匀变速直线运动的实验中,如图所示,为一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的记数点,相邻记数点间的时间间隔T=0.1s.
在研究匀变速直线运动的实验中,如图所示,为一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的记数点,相邻记数点间的时间间隔T=0.1s.