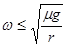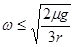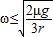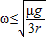题目内容
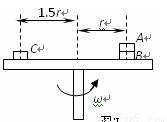
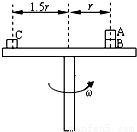
 如图所示,叠放在水平转台上的小物体A、B、C能随转台一起以角速度ω匀速转动,A、B、C的质量分别为3m、2m、m,A与B、B与转台、C与转台间的动摩擦因数都为μ,B、C离转台中心的距离分别为r、1.5r.设本题中的最大静摩擦力等于滑动摩擦力.以下说法中正确的是( )
如图所示,叠放在水平转台上的小物体A、B、C能随转台一起以角速度ω匀速转动,A、B、C的质量分别为3m、2m、m,A与B、B与转台、C与转台间的动摩擦因数都为μ,B、C离转台中心的距离分别为r、1.5r.设本题中的最大静摩擦力等于滑动摩擦力.以下说法中正确的是( )分析:体A随转台一起以角速度ω匀速转动,靠静摩擦力提供向心力,根据牛顿第二定律求出B对A的摩擦力大小.分别对A、AB整体、C受力分析,根据合力提供向心力,求出转台角速度的范围.
解答:解:A、对A受力分析,受重力、支持力以及B对A的静摩擦力,静摩擦力提供向心力,有f=(3m)ω2r≤μ(3m)g.故A错误.
B、由于A与C转动的角速度相同,由摩擦力提供向心力有m×1.5rω2<3mrω2即C与转台间的摩擦力小于A与B间的摩擦力,故B错误;
C、对AB整体,有:(3m+2m)ω2r≤μ(3m+2m)g…①
对物体C,有:mω2(1.5r)≤μmg…②
对物体A,有:3mω2r≤μ(3m)g…③
联立①②③解得:ω≤
,所以C正确D错误.
解得故选C.
B、由于A与C转动的角速度相同,由摩擦力提供向心力有m×1.5rω2<3mrω2即C与转台间的摩擦力小于A与B间的摩擦力,故B错误;
C、对AB整体,有:(3m+2m)ω2r≤μ(3m+2m)g…①
对物体C,有:mω2(1.5r)≤μmg…②
对物体A,有:3mω2r≤μ(3m)g…③
联立①②③解得:ω≤
|
解得故选C.
点评:本题关键是对A、AB整体、C受力分析,根据静摩擦力提供向心力以及最大静摩擦力等于滑动摩擦力列式分析是关键.

练习册系列答案
相关题目