题目内容
6. 将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,想物块悬挂于管口,现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球想转向过程中速率不变.(重力加速度为g)
将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,想物块悬挂于管口,现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球想转向过程中速率不变.(重力加速度为g)(1)求小物块下落过程中的加速度大小;
(2)求小球从管口抛出时的速度大小;
(3)试证明小球平抛运动的水平位移总小于L.
分析 开始时小球沿斜面向上做匀加速,小物块向下也做匀加速,两者的加速度大小相等.对各自受力分析,运用牛顿第二定律列出等式,解出方程.
小物块落地静止不动,小球继续向上做匀减速运动,对其受力分析,运用牛顿第二定律解出此时的加速度(与前一阶段加速度不等),结合运动学公式求出小球从管口抛出时的速度大小.
运用平抛运动的规律表示出小球平抛运动的水平位移,利用数学知识证明问题.
解答 解:(1)设细线中的张力为T,对小球和小物块各自受力分析: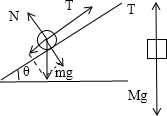
根据牛顿第二定律得:
对M:Mg-T=Ma
对m:T-mgsin30°=ma
且M=km
解得:a=$\frac{2k-1}{2(k+1)}$
(2)设M落地时的速度大小为v,m射出管口时速度大小为v0,M落地后m的加速度为a0.
根据牛顿第二定律有:-mgsin30°=ma0
对于m匀加速直线运动有:v2=2aLsin30°
对于小物块落地静止不动,小球m继续向上做匀减速运动有:v2-v02=2a0L(1-sin30°)
解得:v0=$\sqrt{\frac{k-2}{2(k+1)}gL}$(k>2)
(3)平抛运动x=v0t Lsin30°=$\frac{1}{2}$gt2
解得x=L$\sqrt{\frac{k-2}{2(k+1)}}$
因为$\frac{k-2}{k+1}$<1,所以x<$\frac{\sqrt{2}}{2}$L,得证.
答:(1)小物块下落过程中的加速度大小是$\frac{2k-1}{2(k+1)}$;
(2)小球从管口抛出时的速度大小为$\sqrt{\frac{k-2}{2(k+1)}gL}$;
(3)证明如上
点评 本题考查牛顿第二定律,匀加速运动的公式及平抛运动规律.
要注意第(2)问中要分M落地前和落地后两段计算,因为两段的m加速度不相等.
第(3)问中,因为$\frac{k-2}{k+1}<1$,所以$x=L\sqrt{\frac{k-2}{2(k+1)}}$

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案 在公路的某些路段旁立有交通标志牌,如图甲是路线指示标志,图乙为限速标志,两个标志牌上数字的意思分别是( )
在公路的某些路段旁立有交通标志牌,如图甲是路线指示标志,图乙为限速标志,两个标志牌上数字的意思分别是( )| A. | 甲是指路程,乙是平均速度 | B. | 甲是指路程,乙是瞬时速度 | ||
| C. | 甲是指位移,乙是平均速度 | D. | 甲是指位移,乙是瞬时速度 |

| A. | 该透明材料的临界角是37° | |
| B. | 该透明材料的临界角是53° | |
| C. | 该透明材料的折射率$\frac{5}{4}$ | |
| D. | 该透明材料的折射率$\frac{5}{3}$ | |
| E. | 光线在透明长方体中运动的总时间为$\frac{25R}{2c}$ |
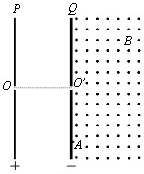 如图17所示,平行金属板P、Q的中心分别有小孔O和O′,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.一质量为m、电荷量为+q的带电粒子,在小孔O处从静止开始做匀加速直线运动.粒子通过小孔O′后,在磁场中做匀速圆周运动,经过半个圆周打在Q板上的A点.不计粒子重力.求:
如图17所示,平行金属板P、Q的中心分别有小孔O和O′,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.一质量为m、电荷量为+q的带电粒子,在小孔O处从静止开始做匀加速直线运动.粒子通过小孔O′后,在磁场中做匀速圆周运动,经过半个圆周打在Q板上的A点.不计粒子重力.求: 质量为m的物体以某以初速度冲上光滑的半径为R的圆弧,则:
质量为m的物体以某以初速度冲上光滑的半径为R的圆弧,则: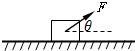 在水平面上,用与水平方向成θ=37°角斜向上方的拉力F=10N拉着一个质量m=1kg的物体从静止开始运动,物体与水平面间的动摩擦因数μ=0.5,物体运动s1=12m时撤去拉力.sin37°=0.6,cos37°=0.8,重力加速度取g=10m/s2.求:
在水平面上,用与水平方向成θ=37°角斜向上方的拉力F=10N拉着一个质量m=1kg的物体从静止开始运动,物体与水平面间的动摩擦因数μ=0.5,物体运动s1=12m时撤去拉力.sin37°=0.6,cos37°=0.8,重力加速度取g=10m/s2.求: 跳台滑雪是勇敢者的运动.它也是冬季奥运会运动项目之一.运动员从倾角为37°的斜面顶端,不借助任何外力沿斜面下滑100m后飞出跳台,平台长度可忽略.(假设斜面光滑,空气阻力不计;sin37°=0.6,cos37°=0.8,g取10m/s2)求:
跳台滑雪是勇敢者的运动.它也是冬季奥运会运动项目之一.运动员从倾角为37°的斜面顶端,不借助任何外力沿斜面下滑100m后飞出跳台,平台长度可忽略.(假设斜面光滑,空气阻力不计;sin37°=0.6,cos37°=0.8,g取10m/s2)求: 回热式制冷机是一种深低温设备,制冷极限约50K.某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为t1=27℃和t2=-133℃;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比( )
回热式制冷机是一种深低温设备,制冷极限约50K.某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为t1=27℃和t2=-133℃;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比( )