题目内容
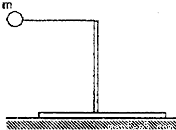 一质量为m的黏性小球,用长为L的细绳挂在一与木块固定在一起的小立柱上,如图所示,木块和立柱的总质量为M,放在水平桌面上,桌面与木块的动摩擦因数为μ.现将小球拉到水平位置后静止释放,与小立柱碰撞后立即粘在小立柱上,设小球在下摆过程中木块不移动.
一质量为m的黏性小球,用长为L的细绳挂在一与木块固定在一起的小立柱上,如图所示,木块和立柱的总质量为M,放在水平桌面上,桌面与木块的动摩擦因数为μ.现将小球拉到水平位置后静止释放,与小立柱碰撞后立即粘在小立柱上,设小球在下摆过程中木块不移动.(1)求碰撞后小球、立柱、木块系统移动的距离;
(2)求小球下摆的过程中,重力的最大功率.
【答案】分析:(1)小球在下摆过程中木块不移动,小球的机械能守恒,由机械能守恒求出碰撞前小球的速度.碰撞过程,时间极短,系统所受的外力可忽略,系统水平方向动量守恒,根据动量守恒求出碰后的速度,再由动能定理列式求出系统移动的距离.
(2)重力的功率等于重力与竖直分速度的乘积,小球下摆的过程中,竖直分速度从零增大再到零,重力功率先增大后减小,则当小球在竖直方向上的加速度为零,即竖直方向上受力平衡,竖直方向上的分速度最大,根据机械能守恒定律、牛顿第二定律和功率公式结合求解.
解答:解:(1)碰撞前瞬间,设小球速度为v,则机械能守恒,得: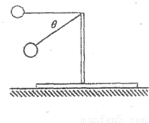
mgl=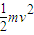
碰撞过程中,系统受的外力冲量很小,可忽略不计,则系统水平方向动量守恒:
mv=(m+M)v′
解得:v′=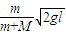
然后,系统在f作用下减速,由动能定理得:
-μ(m+M)gs=0-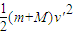
则解出最大位移s=
(2)设小球摆至细绳与水平方向夹角为θ,如图,设此时小球速度为v,
由机械能守恒得:mglsinθ=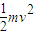 ,得v=
,得v=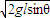 ①
①
由牛顿第二定律得:
T-mgsinθ=m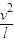 ②
②
重力的功率最大,就是小球在竖直方向上的分速度最大,此时小球在竖直方向上的加速度为零,即竖直方向上受力平衡,所以
Tsinθ=mg ③
联立①解得:sinθ=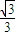
故重力的最大功率:P=mgvcosθ=mg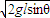 cosθ=
cosθ=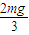
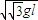
答:
(1)碰撞后小球、立柱、木块系统移动的距离为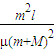 ;
;
(2)小球下摆的过程中,重力的最大功率为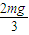
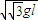 .
.
点评:本题是复杂的力学综合题,把握每个过程的物理规律是基础,关键分析出重力功率最大的条件:竖直方向上受力平衡,也可以采用函数法,由机械能守恒定律和重力的瞬时功率公式得到重力功率与θ的关系式,再求极值.
(2)重力的功率等于重力与竖直分速度的乘积,小球下摆的过程中,竖直分速度从零增大再到零,重力功率先增大后减小,则当小球在竖直方向上的加速度为零,即竖直方向上受力平衡,竖直方向上的分速度最大,根据机械能守恒定律、牛顿第二定律和功率公式结合求解.
解答:解:(1)碰撞前瞬间,设小球速度为v,则机械能守恒,得:

mgl=
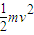
碰撞过程中,系统受的外力冲量很小,可忽略不计,则系统水平方向动量守恒:
mv=(m+M)v′
解得:v′=
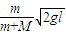
然后,系统在f作用下减速,由动能定理得:
-μ(m+M)gs=0-
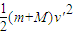
则解出最大位移s=

(2)设小球摆至细绳与水平方向夹角为θ,如图,设此时小球速度为v,
由机械能守恒得:mglsinθ=
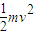 ,得v=
,得v=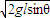 ①
①由牛顿第二定律得:
T-mgsinθ=m
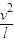 ②
②重力的功率最大,就是小球在竖直方向上的分速度最大,此时小球在竖直方向上的加速度为零,即竖直方向上受力平衡,所以
Tsinθ=mg ③
联立①解得:sinθ=
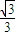
故重力的最大功率:P=mgvcosθ=mg
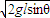 cosθ=
cosθ=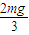
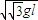
答:
(1)碰撞后小球、立柱、木块系统移动的距离为
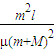 ;
;(2)小球下摆的过程中,重力的最大功率为
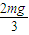
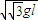 .
.点评:本题是复杂的力学综合题,把握每个过程的物理规律是基础,关键分析出重力功率最大的条件:竖直方向上受力平衡,也可以采用函数法,由机械能守恒定律和重力的瞬时功率公式得到重力功率与θ的关系式,再求极值.

练习册系列答案
相关题目
 (2007?扬州模拟)一质量为m的黏性小球,用长为L的细绳挂在一与木块固定在一起的小立柱上,如图所示,木块和立柱的总质量为M,放在水平桌面上,桌面与木块的动摩擦因数为μ.现将小球拉到水平位置后静止释放,与小立柱碰撞后立即粘在小立柱上,设小球在下摆过程中木块不移动.
(2007?扬州模拟)一质量为m的黏性小球,用长为L的细绳挂在一与木块固定在一起的小立柱上,如图所示,木块和立柱的总质量为M,放在水平桌面上,桌面与木块的动摩擦因数为μ.现将小球拉到水平位置后静止释放,与小立柱碰撞后立即粘在小立柱上,设小球在下摆过程中木块不移动.