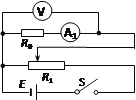
题目内容
【题目】如图所示,一弹性轻绳(绳的弹力与其伸长量成正比)穿过固定的光滑圆环B,左端固定在A点,右端连接一个质量为m的小球,A、B、C在一条水平线上,弹性绳自然长度为AB。小球穿过竖直固定的杆,从C点由静止释放,到D点时速度为零,C、D间距离为h。已知小球在C点时弹性绳的拉力为0.5mg,g为重力加速度,小球和杆间动摩擦因素为0.5,弹性绳始终处在弹性限度内,下列说法正确的是( )
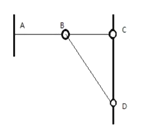
A. 小球从C点运动到D点的过程中克服摩擦力做功为0.5mgh
B. 若在D点给小球一个向上的速度v,小球恰好回到C点,则![]()
C. 若仅把小球的质量变成2m,则小球到达D点的速度大小为![]()
D. 若仅把小球的质量变成2m,则小球向下运动到速度为零的位置与C点距离为2h
【答案】BC
【解析】A、在D点对小球进行受力分析,如图所示:
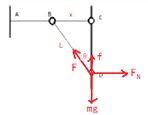
则![]() ,则
,则 ![]() ,
,
则摩擦力功为: ![]() ,故选项A错误;
,故选项A错误;
B、从C到D点后,在返回C点,根据动能定理: ![]() ,则
,则![]() ,故选项B正确;
,故选项B正确;
C、当质量为m时,从C到D根据动能定理: ![]()
则: ![]()
若仅把小球的质量变成![]() ,从C到D根据动能定理:
,从C到D根据动能定理: ![]()
则: ![]() ,故选项C正确;
,故选项C正确;
D、若仅把小球的质量变成![]() ,则小球向下运动到速度为零时,则弹簧做功变大,且无法求出,故小球下落最终位置无法求出,故选项D错误。
,则小球向下运动到速度为零时,则弹簧做功变大,且无法求出,故小球下落最终位置无法求出,故选项D错误。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目