题目内容
3. 在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求:
在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求:(1)电场强度E的大小;
(2)小球从M点开始运动到第二次经过D点所用的时间;
(3)小球运动的周期,并画出运动轨迹(只画一个周期).
分析 (1)小球从M点运动到N点时,电场力与重力平衡,由平衡条件即可求解E的大小;
(2)根据直线运动与圆周运动,结合运动学公式与周期公式,即可求解;
(3)由上分析,根据受力与运动情况,可画出运动轨迹.
解答  解:(1)小球从M点运动到N点时,有qE=mg,解得 E=$\frac{mg}{q}$.
解:(1)小球从M点运动到N点时,有qE=mg,解得 E=$\frac{mg}{q}$.
(2)小球从M点到达N点所用时间t1=t0
小球从N点经过$\frac{3}{4}$个圆周,到达P点,所以 t2=t0
小球从P点运动到D点的位移 x=R=$\frac{m{v}_{0}}{q{B}_{0}}$
小球从P点运动到D点的时间 t3=$\frac{R}{{v}_{0}}$=$\frac{m}{{B}_{0}q}$
得 t0=$\frac{2πm}{qB}$,t3=$\frac{2{t}_{0}}{3π}$
所以所求时间 t=t1+t2+t3=2t0($\frac{1}{3π}$+1).
(3)小球运动一个周期的轨迹如图所示.小球的运动周期为T=8t0.
答:
(1)电场强度E的大小是$\frac{mg}{q}$;
(2)小球从M点开始运动到第二次经过D点所用的时间是2t0($\frac{1}{3π}$+1);
(3)小球运动的周期是8t0,画出运动轨迹如图所示.
点评 考查粒子在复合场的运动,掌握受力与运动的关系,注意学会画出运动轨迹,体现几何的特性及对称性.

练习册系列答案
相关题目
11. 如图所示.轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A静止于光滑水平桌面上,右端接一细线,细线绕过光滑的定滑轮与物体B相连.开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )
如图所示.轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A静止于光滑水平桌面上,右端接一细线,细线绕过光滑的定滑轮与物体B相连.开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )
 如图所示.轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A静止于光滑水平桌面上,右端接一细线,细线绕过光滑的定滑轮与物体B相连.开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )
如图所示.轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A静止于光滑水平桌面上,右端接一细线,细线绕过光滑的定滑轮与物体B相连.开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )| A. | B物体的动能增加量小于B物体重力势能的减少量 | |
| B. | B物体机械能的减少量等于弹簧的弹性势能的增加量 | |
| C. | 细线拉力对A做的功等于A物体与弹簧所组成的系统机械能的增加量 | |
| D. | 合力对A先做正功后做负功 |
18. 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )| A. | W1=$\frac{mg}{2h}$(h2-R2) | B. | W2=GR(1-$\frac{R}{h}$) | C. | W1=$\frac{hKQq}{{R}^{2}}$(1-$\frac{R}{h}$) | D. | G=$\frac{khQq}{{R}^{2}}$ |
8.下列说法正确的是( )
| A. | ${\;}_{15}^{30}$P→${\;}_{14}^{30}$Si+${\;}_{1}^{0}$e是一种核裂变反应 | |
| B. | 核反应堆产生的能量一定来自轻核聚变 | |
| C. | 太阳辐射的能量主要来自太阳内部的核裂变反应 | |
| D. | 卢瑟福为解释α粒子散射实验现象提出了原子核式结构学说 |
15.在电磁学发展过程中,许多科学家作出了贡献,下列说法正确的是( )
| A. | 奥斯特发现了电流磁效应;法拉第发现了电磁感应现象 | |
| B. | 麦克斯韦预言了地磁波;楞次用实验证实了地磁波的存在 | |
| C. | 昆仑发现了点电荷的相互作用规律;密立根发现了磁场对电流的作用规律 | |
| D. | 安培发现了磁场对运动电荷的作用规律;洛仑兹发现了磁场对电流的作用规律 |
13.一质点开始时做匀速直线运动,从某时刻起受到一恒力作用.此后,该质点的动能不可能( )
| A. | 一直增大 | |
| B. | 先逐渐增大至某一最大值,再逐渐减小 | |
| C. | 先逐渐减小至零,再逐渐增大 | |
| D. | 先逐渐减小至某一非零的最小值,再逐渐增大 |

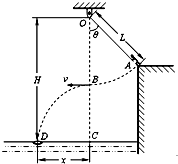 某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)
