题目内容
14.质量为m的汽车,以速度v通过半径为R的凹形桥的底端时,它对桥的压力为( )| A. | m(g+$\frac{{v}^{2}}{R}$) | B. | m(g-$\frac{v^2}{R}$) | C. | m($\frac{v^2}{R}$-g) | D. | mg |
分析 在最低点,靠汽车的重力和支持力提供向心力,根据牛顿第二定律求出汽车对桥面的压力.
解答 解:对于凹形桥最低点,根据牛顿第二定律得:FN-mg=m$\frac{{v}^{2}}{R}$
得:FN=mg+m$\frac{{v}^{2}}{R}$
根据牛顿第三定律可知,在桥面最低点时汽车对桥面的压力大小为m(g+$\frac{{v}^{2}}{R}$).
故选:A
点评 解决本题的关键知道做圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大,属于基础题.

练习册系列答案
相关题目
6.下列所描述的运动的中,不可能的有( )
| A. | 速度变化很大,加速度很小 | |
| B. | 速度变化方向为正,加速度方向为负 | |
| C. | 速度越来越大,加速度越来越小 | |
| D. | 速度变化越来越快,加速度越来越大 |
 如图1所示,水平转盘上放有质量为m=1kg的小物块,小物块到转轴的距离为r=0.5m,连接小物块和转轴的绳刚好被拉直(绳中张力为零),小物块和转盘间的最大静摩擦力是其重力的k=0.2倍.g=10m/s2,求:
如图1所示,水平转盘上放有质量为m=1kg的小物块,小物块到转轴的距离为r=0.5m,连接小物块和转轴的绳刚好被拉直(绳中张力为零),小物块和转盘间的最大静摩擦力是其重力的k=0.2倍.g=10m/s2,求: 如图所示,滑板车运动现在深受青少年喜爱.某同学站在滑板车上从静止开始以a=2m/s2的加速度沿斜坡匀加速直线滑下,经过t=3s的时间,该同学的速度达到多大?
如图所示,滑板车运动现在深受青少年喜爱.某同学站在滑板车上从静止开始以a=2m/s2的加速度沿斜坡匀加速直线滑下,经过t=3s的时间,该同学的速度达到多大? 如图所示,ABCD为倾角为30°的足够长光滑绝缘斜面,EFGH范围内存在磁感应强度为B=1T、方向垂直斜面的匀强磁场,磁场的宽度为d=1.9m,边界EF、HG与斜面底边AB平行.一边长为L=1m、电阻为R=1Ω、质量为m=1kg的正方形金属框MNPQ放在斜面上,MN边与磁场上边界平行且距离为b=1.5m,重力加速度为g=10m/s2,现使金属框由静止释放,在金属框MN边刚出磁场时恰好做匀速直线运动.求:
如图所示,ABCD为倾角为30°的足够长光滑绝缘斜面,EFGH范围内存在磁感应强度为B=1T、方向垂直斜面的匀强磁场,磁场的宽度为d=1.9m,边界EF、HG与斜面底边AB平行.一边长为L=1m、电阻为R=1Ω、质量为m=1kg的正方形金属框MNPQ放在斜面上,MN边与磁场上边界平行且距离为b=1.5m,重力加速度为g=10m/s2,现使金属框由静止释放,在金属框MN边刚出磁场时恰好做匀速直线运动.求: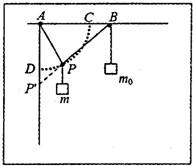 某学习小组设计了一种粗测小物体质量的方法.使用的器材有细绳、硬纸板、支架、刻度尺、铅笔、白纸、自制小滑轮、已知质量的小物块和若干待测小物体等.简化的实验装置如图所示,在A点固定一根细绳AP,以A为圆心、AP为半径描出圆弧CD,直线AC水平,AD竖直.在B点固定小滑轮,一根细绳绕过小滑轮,一端悬挂小物块(质量m0已知),另一端连接绳端P点.在结点P悬挂不同质量的待测小物体m,
某学习小组设计了一种粗测小物体质量的方法.使用的器材有细绳、硬纸板、支架、刻度尺、铅笔、白纸、自制小滑轮、已知质量的小物块和若干待测小物体等.简化的实验装置如图所示,在A点固定一根细绳AP,以A为圆心、AP为半径描出圆弧CD,直线AC水平,AD竖直.在B点固定小滑轮,一根细绳绕过小滑轮,一端悬挂小物块(质量m0已知),另一端连接绳端P点.在结点P悬挂不同质量的待测小物体m,