题目内容
如图所示，一条轻弹簧和一根细线共同拉住一个质量为m的小球，平衡时细线水平，弹簧与竖直方向的夹角是θ，则弹簧拉力的大小为______．若突然剪断细线，则在刚剪断的瞬间，小球的加速度大小为______．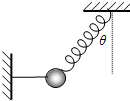
根据共点力平衡得，弹簧的弹力F=
．绳子的拉力T=mgtanθ．
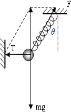
剪断细线的瞬间，弹簧的弹力不变，则弹簧弹力和重力的合力与绳子的拉力等值反向，根据牛顿第二定律得，a=
=
=gtanθ．
故答案为：
；gtanθ
| mg |
| cosθ |
剪断细线的瞬间，弹簧的弹力不变，则弹簧弹力和重力的合力与绳子的拉力等值反向，根据牛顿第二定律得，a=
| F合 |
| m |
| mgtanθ |
| m |
故答案为：
| mg |
| cosθ |
练习册系列答案
相关题目
如图所示，一条轻弹簧和一根细线共同拉住一个质量为m的小球，平衡时细线水平，弹簧与竖直方向的夹角是θ，则弹簧拉力的大小为
如图所示，一条轻弹簧和一根细线共同拉住一个质量为m的小球，平衡时细线水平，弹簧与竖直方向的夹角是θ，则弹簧拉力的大小为________．若突然剪断细线，则在刚剪断的瞬间，小球的加速度大小为________．