题目内容
如图所示，细线与竖直线的夹角θ=30°，一条长为l的绳，一端固定在顶点O，另一端系一个质量为m的小球（视作质点），小球以某一速率绕竖直线做水平匀速圆周运动求（1）绳子对小球的拉力T=？；
（2）小球做水平匀速圆周运动速率v=？
分析：（1）小球绕竖直线做水平匀速圆周运动，由合力提供其向心力．分析受力情况，根据力的合成法求解拉力T的大小．
（2）根据牛顿第二定律和向心力公式列式，求出小球做水平匀速圆周运动速率v．
（2）根据牛顿第二定律和向心力公式列式，求出小球做水平匀速圆周运动速率v．
解答：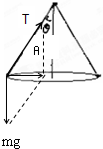
解：（1）小球绕竖直线做水平匀速圆周运动，受到重力和细线的拉力，由合力提供其向心力．
由cosθ=
得：T=
=
mg
（2）由牛顿运动定律可知 mgtanθ=m
又半径r=lsinθ
解得：v=
=
=
答：
（1）绳子对小球的拉力T=
mg；
（2）小球做水平匀速圆周运动速率v=
．
解：（1）小球绕竖直线做水平匀速圆周运动，受到重力和细线的拉力，由合力提供其向心力．由cosθ=
| mg |
| T |
| mg |
| cosθ |
2
| ||
| 3 |
（2）由牛顿运动定律可知 mgtanθ=m
| v2 |
| r |
又半径r=lsinθ
解得：v=
| grtanθ |
| glsinθtanθ |
|
答：
（1）绳子对小球的拉力T=
2
| ||
| 3 |
（2）小球做水平匀速圆周运动速率v=
|
点评：解决本题的关键分析物体的受力情况，确定出向心力的来源，准确确定半径，以及能够熟练运用牛顿第二定律求解．
练习册系列答案
相关题目
（2006?松江区二模）学过单摆的周期公式以后，物理兴趣小组的同学们对钟摆产生了兴趣，老师建议他们先研究用厚度和质量分布均匀的方木块（如一把米尺）做成的摆（这种摆被称为复摆），如图所示．让其在竖直平面内做小角度摆动，C点为重心，板长为L，周期用T表示．
如图所示，水平地面上竖直地固定着一个光滑的圆环，一个质量为m的小球套在环上，圆环最高点有一小孔，细线一端被人牵着，另一端穿过小孔与小球相连，使球静止于A处，此时细线与竖直成θ角，重力加速度为g，则不正确的说法是（ ）
（2008?广州模拟）如图所示的轨道由位于竖直平面的圆弧轨道和水平轨道两部分相连而成．水平轨道的右侧有一质量为2m的滑块C与轻质弹簧的一端相连，弹簧的另一端固定在竖直的墙M上，弹簧处于原长时，滑块C在P点处；在水平轨道上方O处，用长为L的细线悬挂一质量为m的小球B，B球恰好与水平轨道相切于D点，并可绕D点在竖直平面内摆动．质量为m的滑块A由圆弧轨道上静止释放，进入水平轨道与小球B发生碰撞，A、B碰撞前后速度发生交换．P点左方的轨道光滑、右方粗糙，滑块A、C与PM段的动摩擦因数均为μ=
如图所示，细线上端固定于O点，其下端系一小球，静止时细线长L．现将悬线和小球拉至图中实线位置，此时悬线与竖直方向的夹角θ=60°，并于小球原来所在的最低点处放置一质量相同的泥球，然后使悬挂的小球从实线位置由静止释放，它运动到最低点时与泥球碰撞并合为一体，它们一起摆动中可达到的最大高度是（ ）