题目内容
甲、乙两辆汽车行驶在同一条子直公路上,甲车在乙车后面做速度为v的匀速运动,乙车在甲车前面做初速度为零的匀加速运动,加速度为a,两车同向而行,开始时两车相距x,为使两车可相遇两次,求v、a、x所满足的关系式.
答案:略
解析:
解析:
|
因为甲车在后面做匀速直线运动,只要甲车在一定时间内能超过乙车,而乙车做的是匀加速直线运动,再经一段时间乙车必能追上甲车,这样两车就会有两次相遇. 设在时间 t内甲车追上了乙车,则应有:
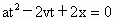 ,所以 ,所以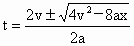 . .
由题意, t应为实数,所以可得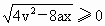 ,即 ,即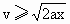 .要使两车相遇两次,则t应有两个正的实数解.上式中应将等号去掉,即 .要使两车相遇两次,则t应有两个正的实数解.上式中应将等号去掉,即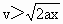 .此式中已隐含了 .此式中已隐含了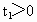 , ,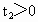 .故v、a、x只要满足 .故v、a、x只要满足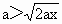 ,则甲、乙两车就可相遇两次. ,则甲、乙两车就可相遇两次.
本题所研究的是多次相遇问题,解决方法一般是列出关于时间 t的位移关系式,然后利用判别式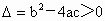 是一元二次方程有两个实数解(其中两解乘积为正,求和为正)的条件,从而即可判定两物体可二次相遇. 是一元二次方程有两个实数解(其中两解乘积为正,求和为正)的条件,从而即可判定两物体可二次相遇.
在下述几种情况下可出现二次相遇的问题: 做匀速直线运动的物体追击做匀加速直线运动的物体时,可能出现两次相遇. 做匀减速直线运动的物体追击做匀速直线运动的物体时,可能出现两次相遇. 做匀减速直线运动的物体追击做匀加速直线运动的物体时,可能出现两次相遇. 做匀加速直线运动的物体之间的相互追击,乃至于做匀减速直线运动的物体之间的相互追击均有可能出现两次相遇. |

练习册系列答案
相关题目
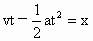
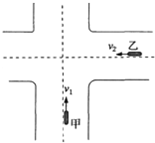 据统计城市交通事故大多因违章引起.甲、乙两辆汽车分别在相互垂直的道路上,沿各自道宽的中心线(图中虚线所示)向前匀速行驶,当甲、乙两车的车头到十字路口(道路中心线)的距离分别为30米和40米时.道口恰处于红、绿灯转换.甲、乙两车均未采取任何减速或制动等措施,以至两车相撞.已知两车型号相同,汽车的车长为5.2米,车宽为1.76米.并已知甲车的速度为V1=40公里/小时,设两车相撞前均匀速行驶.试判断在穿过路口过程中,乙车车速的范围为
据统计城市交通事故大多因违章引起.甲、乙两辆汽车分别在相互垂直的道路上,沿各自道宽的中心线(图中虚线所示)向前匀速行驶,当甲、乙两车的车头到十字路口(道路中心线)的距离分别为30米和40米时.道口恰处于红、绿灯转换.甲、乙两车均未采取任何减速或制动等措施,以至两车相撞.已知两车型号相同,汽车的车长为5.2米,车宽为1.76米.并已知甲车的速度为V1=40公里/小时,设两车相撞前均匀速行驶.试判断在穿过路口过程中,乙车车速的范围为 据统计,城市交通事故大多因违章引起,在如图所示中,甲、乙两辆汽车分别在相互垂直的道路上,沿各自道宽的中心线(图中虚线所示)向前匀速行驶,当甲、乙两车的车头到十字路口(道路中心线)的距离分别为30m、40m时,道口恰处于红、绿灯转换甲、乙两车均未采取任何减速或制动等措施,以致两车相撞.已知两车型号相同,汽车的车长为5.2m,车宽为1.76m.并已知甲车的车速为v1=40km/h,设两车相撞前均匀速行使.试判断在穿过路口过程中,乙车车速的范围.
据统计,城市交通事故大多因违章引起,在如图所示中,甲、乙两辆汽车分别在相互垂直的道路上,沿各自道宽的中心线(图中虚线所示)向前匀速行驶,当甲、乙两车的车头到十字路口(道路中心线)的距离分别为30m、40m时,道口恰处于红、绿灯转换甲、乙两车均未采取任何减速或制动等措施,以致两车相撞.已知两车型号相同,汽车的车长为5.2m,车宽为1.76m.并已知甲车的车速为v1=40km/h,设两车相撞前均匀速行使.试判断在穿过路口过程中,乙车车速的范围.