��Ŀ����
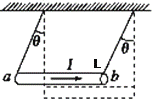
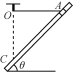
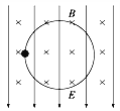
����Ŀ����ͼ��ʾ������ֱƽ�����������ƽ�С�������Բ��ƵĽ������죨�㹻�������ڵ���������ֵ�ֱ�ΪR1��R2���������裬һ������Ϊm�Ľ�����ab��ֱ����������ϣ�����װ�ô��ڴ�ֱ��������ƽ�����ǿ�ų��С����ý�����ab�ص����ɾ�ֹ��ʼ�˶�����ֻ�պϿ���S1��������ab�»��ܴﵽ������ٶ�Ϊ![]() ����ֻ�պϿ���S2��������ab�»��߶�Ϊhʱǡ�ôﵽ�ܴﵽ������ٶ�Ϊ
����ֻ�պϿ���S2��������ab�»��߶�Ϊhʱǡ�ôﵽ�ܴﵽ������ٶ�Ϊ![]() ���������ٶ�Ϊg����
���������ٶ�Ϊg����
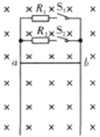
��1���������ĵ���r��
��2��������ab�ɾ�ֹ��ʼ���ﵽ����ٶ�![]() �Ĺ����У�ͨ������R2�ĵ����Q��
�Ĺ����У�ͨ������R2�ĵ����Q��
��3��������ab�ɾ�ֹ��ʼ���ﵽ����ٶ�![]() ���õ�ʱ�䣻
���õ�ʱ�䣻
��4�����ý�����ab�ص����ɾ�ֹ��ʼ�˶���ͬʱ�պϿ���S1��S2��������ab�»��߶�Ϊ![]() ʱ�ﵽ������ٶ�Ϊv�����ԱȽ�h��
ʱ�ﵽ������ٶ�Ϊv�����ԱȽ�h��![]() ��v2��v���Ĵ�С��ϵ���������Ƶ���ֱ��д�������
��v2��v���Ĵ�С��ϵ���������Ƶ���ֱ��д�������
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]() ��4��
��4��![]() >
>![]() h>h��
h>h��
��������
��1������ǿ�ų��ĴŸ�Ӧǿ��ΪB�������ľ���ΪL����
���������ﵽ����ٶ�![]() ʱ��
ʱ��
��ƽ��������![]()
�ɱպϵ�·��ŷķ���ɿɵ�![]()
�����Ϸ��̽�ã�![]()
���������ﵽ����ٶ�![]() ʱ��ͬ���У�
ʱ��ͬ���У� ![]()
��ã� ![]()
��2����![]() ����
����![]() ����ã�
����ã�![]()
���ݷ����ڵ�Ÿ�Ӧ���ɿɵ�ƽ����Ӧ�綯��Ϊ��
ȫ����ab�ɾ�ֹ��ʼ���ﵽ����ٶ�![]() �Ĺ����У���ƽ����Ӧ�綯��Ϊ��
�Ĺ����У���ƽ����Ӧ�綯��Ϊ�� ![]()
��ƽ������Ϊ��![]()
���![]()
��ã�![]()
��3���������Ӿ�ֹ������ٶȹ����У��ɶ��������У�
![]()
����![]()
�����![]()
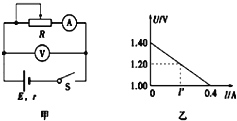
��4�������ΰ��Ħ�- tͼ���֪
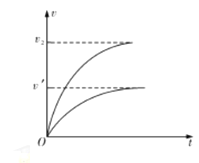
![]()
![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�