题目内容
利用以下信息：地球半径为R，地球表面的重力加速度为g，以无穷远处为零势能面，距离地心为r、质量为m的物体势能为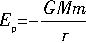
（其中M为地球质量，G为万有引力常量），求解下列问题：某卫星质量为m，在距地心为2R的轨道上做圆周运动，在飞行的某时刻，卫星向飞行的相反方向弹射出质量为
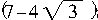m的物体后，卫星做离心运动.若被弹射出的物体恰能在原来轨道上做相反方向的匀速圆周运动，则卫星的飞行高度变化多少？
设卫星在距地心为2R的轨道上运行时速率为v0，则有
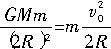①若设卫星将小物体反向弹出后的瞬时速率为v1，由动量守恒定律得
②如果卫星在离地心较远轨道r上，运行的速率用v2表示，设m′=m-
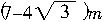m，则有
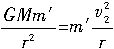③由于卫星做离心运动后遵守系统机械能守恒定律，故有
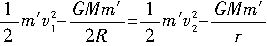④解①②③④得r=3R，显然卫星飞行高度的变化量
Δh=r-2R=R
【试题分析】
练习册系列答案
名校课堂系列答案
相关题目
（2012?海淀区模拟）北斗卫星导航系统是我国正在自主研发的全球卫星导航系统，该系统由空间端（卫星）、地面端（中心控制系统）和用户端（导航定位仪）三部分组成，预计2020年形成全球覆盖能力．目前正在试用的“北斗一号”卫星导航试验系统也称“双星定位导航系统”，利用两颗地球同步静止轨道卫星为用户提供快速定位导航服务．