题目内容
1.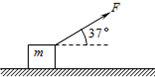 如图所示,质量为2kg的金属块放在水平地面上,在大小为20N、方向与水平方向成37°角的斜向上拉力F作用下,从静止开始做匀加速直线运动.已知金属块与地面间的动摩擦因数μ=0.5,力F持续作用2s后撤去.(sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2).求:金属块在地面上总共滑行了多远?
如图所示,质量为2kg的金属块放在水平地面上,在大小为20N、方向与水平方向成37°角的斜向上拉力F作用下,从静止开始做匀加速直线运动.已知金属块与地面间的动摩擦因数μ=0.5,力F持续作用2s后撤去.(sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2).求:金属块在地面上总共滑行了多远?
分析 对物体受力分析后,根据牛顿第二定律列式求解加速度,根据位移时间关系公式列式求解,根据牛顿第二定律求解出加速度,再根据速度位移公式求解位移.
解答 解:根据牛顿定律有
水平方向:F•cos37°-f=ma
竖直方向:N=mg-F•sin37°
其中f=μN
得:F•cos37°-μ(mg-F•sin37°)=ma1
代入数据解得:a1=6m/s2
则:V1=a1t=12m/s
x1=$\frac{1}{2}$a1t2
代入数据解得:X1=12m
撤去力F后物体的加速度为:a2=μg=5m/s2
由vt2-v02=2ax2
带入数据解得:x2=14.4m
则:金属块在地面上总共滑行了x=x1+x2=26.4m
答:金属块在地面上总共滑行了26.4m.
点评 本题关键是多次根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解运动学参量.

练习册系列答案
相关题目
12.下列有关“温度”的说法中,正确的是( )
| A. | 温度反映了每个分子热运动的剧烈程度 | |
| B. | 温度是分子平均动能的标志 | |
| C. | 温度变化1K等同于温度变化1℃ | |
| D. | 温度升高时物体的每个分子的动能都将增大 |
9.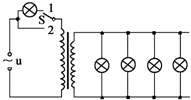 有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
 有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )
有5个完全相同的灯泡连接在理想变压器的原、副线圈中,如图所示.若将该线路与交流电源接通,且开关S接在位置1时,5个灯泡发光亮度相同;若将开关S接在位置2时,灯泡均未烧坏.则下列可能的是( )| A. | 该变压器是降压变压器,原、副线圈匝数比为4:1 | |
| B. | 该变压器是升压变压器,原、副线圈匝数比为1:4 | |
| C. | 副线圈中的灯泡仍能发光,只是更亮些 | |
| D. | 副线圈中的灯泡仍能发光,只是亮度变暗 |
16.质量为m的汽车以恒定功率P启动后沿水平道路行驶,经过一段时间后将达到最大速度v.若行驶中受到的摩擦阻力大小不变,则在加速过程中车速为$\frac{1}{3}$v时,汽车的加速度大小为( )
| A. | $\frac{3P}{mv}$ | B. | $\frac{2P}{mv}$ | C. | $\frac{P}{mv}$ | D. | $\frac{4P}{mv}$ |
13.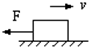 如图所示,在水平面上有一个向右运动的物体,物体的质量为20kg,与水平面间的动摩擦因数为0.1,它在运动过程中还受到一个水平向左的大小为10N的拉力作用,则物体所受滑动摩擦力的大小为( )
如图所示,在水平面上有一个向右运动的物体,物体的质量为20kg,与水平面间的动摩擦因数为0.1,它在运动过程中还受到一个水平向左的大小为10N的拉力作用,则物体所受滑动摩擦力的大小为( )
 如图所示,在水平面上有一个向右运动的物体,物体的质量为20kg,与水平面间的动摩擦因数为0.1,它在运动过程中还受到一个水平向左的大小为10N的拉力作用,则物体所受滑动摩擦力的大小为( )
如图所示,在水平面上有一个向右运动的物体,物体的质量为20kg,与水平面间的动摩擦因数为0.1,它在运动过程中还受到一个水平向左的大小为10N的拉力作用,则物体所受滑动摩擦力的大小为( )| A. | 10N,水平向右 | B. | 10N,水平向左 | C. | 20N,水平向右 | D. | 20N,水平向左 |
10.有两颗地球同步卫星,下列关于它们的说法正确的是( )
| A. | 轨道半径可以不同 | |
| B. | 线速度大小可以不同 | |
| C. | 均有可能通过滕州上空 | |
| D. | 运行的线速度一定小于第一宇宙速度 |
11.今将同一根条形磁铁缓慢地或迅速地全部插入一闭合线圈中,试比较在上述两过程中,相同的物理量是( )
| A. | 磁通量的变化量 | B. | 外力所做的功 | ||
| C. | 感应电动势的平均值 | D. | 通过线圈导线横截面的电量 |
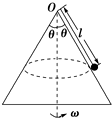 如图所示,用一根长为L=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑椎体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10m/s2,结果可用根式表示)求:
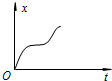
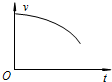
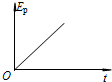
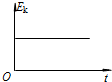
如图所示,用一根长为L=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑椎体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10m/s2,结果可用根式表示)求: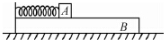 如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.对于木板B从静止开始运动到第一次与物块A速度相等的过程中,若用x、v分别表示物块A的位移和速度的大小,用Ep、Ek分别表示弹簧的弹性势能和A、B的动能之和,用t表示时间,则下列图象可能正确的是( )
如图所示,放置在水平地面上的木板B的左端固定一轻弹簧,弹簧右端与物块A相连.已知A、B质量相等,二者处于静止状态,且所有接触面均光滑.现设法使物块A以一定的初速度沿木板B向右运动,在此后的运动过程中弹簧始终处在弹性限度内,且物块A始终在木板B上.对于木板B从静止开始运动到第一次与物块A速度相等的过程中,若用x、v分别表示物块A的位移和速度的大小,用Ep、Ek分别表示弹簧的弹性势能和A、B的动能之和,用t表示时间,则下列图象可能正确的是( )